实践是检验真理的唯一途径。上一篇博文定量分析了动量加速梯度递减收敛，本文章从实践角度， 验证此特性。针对逻辑回归和线性回归，分别做了四组试验：

  • gd 梯度递减
  • sgd 随机梯度递减
  • gd_m 动量梯度递减
  • sgd_m 动量随机梯度建

在R中，使用了iris，mtcars和学位申请数据。由于线性回归得到的效果与逻辑回归一致，动量均有显著的加速效果，所以下面只显示逻辑回归的实验效果，线性回归试验参考这里。

实验1：学位申请数据

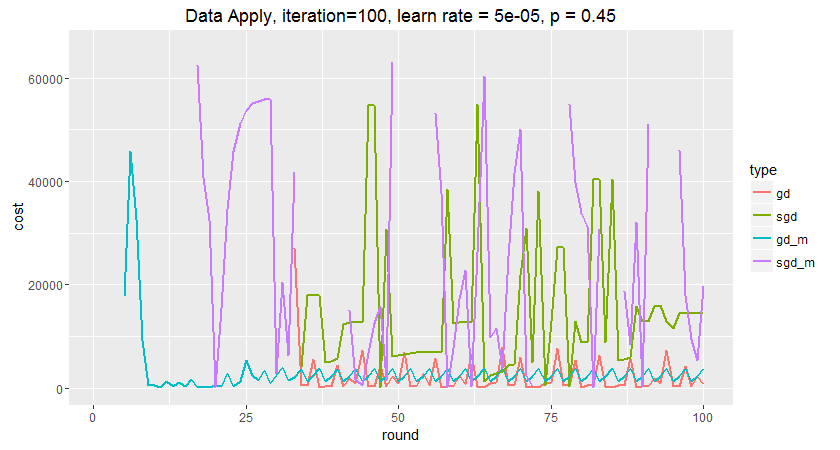
横轴是迭代轮数，纵轴是损失值。虽然四条线均有明显波动，但是开始可以看到动量梯度递减gd_m收敛非常快，且比较平稳；紧接着是随机版sgd_m，但是其波动非常大；梯度递减gd落后非常明显，但是后面也较平稳；随机梯度递减效果不太理想，基本上没有收敛。

实验2：R内置数据iris

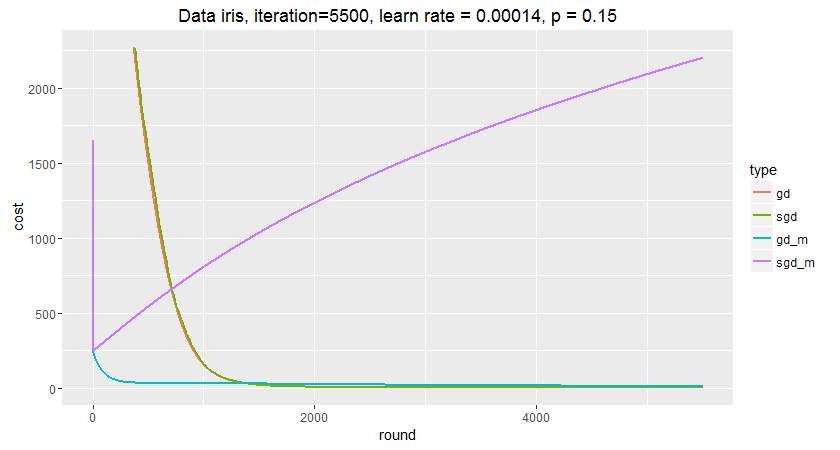
gd与sgd的曲线吻合比较好，在1200轮时达到拐点;gd_m收敛明显快与gd和sgd,在200轮时就达到最低点，但是在1400轮时，效果变差了，而且随着轮数增加，损失函数有向高增长的趋势。sgd_m的表现非常有意思，在50轮以内迅速达到拐点，然后一路走高，损失非常高。

实验3：R内置数据mtcars

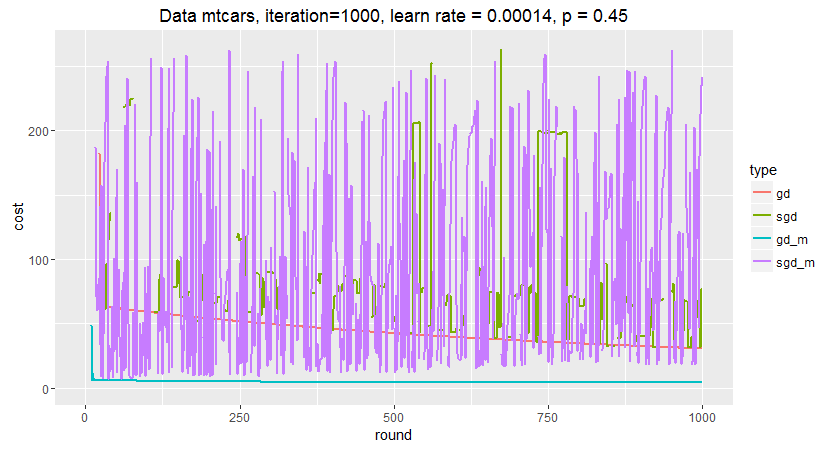
两个随机版本版本波动非常大，而且sgd_m的趋势与实验2类似，有走高趋势。gd_m收敛速度和程度均大于gd。

总结

根据上面的实验，动量对梯度递减收敛效果总结如下

  • 动量的确可以加速梯度递减收敛。
  • 动量随机梯度递减波动非常大，但是收敛速度也比gd和sgd快。
  • 动量梯度递减后期会增加损失函数，需要提早结束。
  • 虽然理论上在p在0.9附近效果较好；但上面的实验却不是，在实验过程中，如果p=0.9,损失会快速发散，没有优化效果。

逻辑回归损失函数是凸函数，只有全局最优。后面有机会，可以使尝试非凸函数。从之前的理论分析来看，动量应该仅仅使得加速收敛到局部最优；对冲破局部最优，达到全局最优无能为力。