动量加快梯度递减收敛--理论篇
背景
最近一段时间在看了一篇梯度递减优化论文,使用物理中的动量概念(Momentum)降低梯度递减的收敛轮数。回忆一下高中物理,动量就是物体速度与质量的乘积。从物理角度解决优化问题(模拟退火属于这类),觉得还是挺有意思的,所以仔细的读完了全文,并且证明了论文中略过的推导,同时还做了一些实验,验证此理论。本文主要梳理整个推导过程,并记录文章略过的推导过程,希望对理解该文章有用。下一篇文章分享相关实验。
物理的角度类比梯度下降有其合理性。梯度下降可以想象为一个小石子,从较高的山坡往下滚动,当达到比较低的地方就停下来了,此时重力势能降到最低,动能为0。开销函数的初始值,可以认为是最开始的重力势能。
我们下面要讨论是用阻力谐振子的物理模型分析梯度下降,阻力谐振子模型在现实生活中也很常见。比如树枝随风摇摆,防火门自动关闭等,均可以用此模型分析,示意图如下
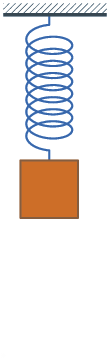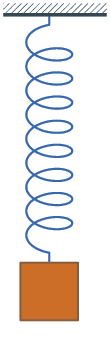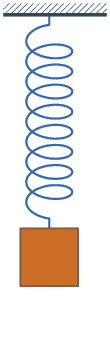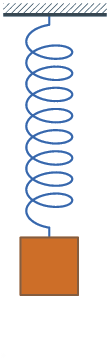
阻力谐振子模型与梯度递减的关系
(下面的所有数学公式编号与原论文保持一致,方便对比论文阅读)
回忆梯度递减的优化方法,沿着梯度的反方向修改权重向量$w$
\[\Delta w_t = -\epsilon \nabla_w E(w_t) \qquad (1)\]其中 $\epsilon$为学习率,$w$为权重向量。如果考虑动量,算法修改如下
\[\Delta w_t = -\epsilon \nabla_w E(w_t) + p\Delta w_{t-1} \quad (2)\]唯一的区别是每轮修改考虑了上一轮梯度变化的情况$p\Delta w_{t-1}$。
论文从阻力谐振子模型的角度进行类比,发现如果振子质量为0,此模型与梯度递减形式一致。
阻力谐振子描述的一个有重量,无体积的物体,在粘性介质中,受到弹性力的作用,在一维的情况下,其受力方程可以如下表示
\[m \ddot{x} = -c \dot{x} - kx\]即质量($m$)与加速度($\ddot{x}$)乘积等于物体当前的受力情况。而物体在粘性介质中,并且受到弹簧牵引。粘性介质阻力正比于速度($\dot{x}$),方向相反;弹簧弹力正比位移($x$),方向相反。$c$为粘性介质系数,$k$为弹簧弹性系数。
再回忆一下高中物理,弹性势能可以表示如下
\[E(x) = \int_{x}^0 -kx dx = \frac{1}{2}kx^2\]如果对位移x求导,可以得到弹力大小,
\[\nabla_x E(x) = kx\]所以,如果将上面$x$全部替换为高纬度位移向量$w$,并代入上面的受力方程,得到如下公式
\[m \frac{d^2 w}{d t^2} = - \mu\frac{dw}{dt} -\nabla_wE(w) \qquad (4)\]将速度和加速度离散化,速度的离散形式
\[v_t = \frac{dw}{dt} = \frac{w_{t+\Delta t} - w_t}{\Delta t}\]加速度的离散形式
\[\frac{d^2w}{dt^2} = \frac{v_t - v_{t-1}}{\Delta t} = \frac{w_{t+\Delta t}+ w_{t-\Delta t} - 2w_t}{(\Delta t) ^2}\]将离散化的变量代入(4)
\[m \frac{w_{t+\Delta t}+ w_{t-\Delta t} - 2w_t}{(\Delta t) ^2} = - \mu \frac{w_{t+\Delta t} - w_t}{\Delta t} -\nabla_wE(w) \qquad (5)\]整理(5),如下
\[w_{t+\Delta t} - w_t = - \frac{(\Delta t)^2}{m+\mu \Delta t} \nabla_w E(w) + \frac{m}{m+\mu\Delta t}(w_t - w_{t-\Delta t}) \qquad(6)\]将系数用符号替代,
\[\epsilon = \frac{(\Delta t)^2}{m+\mu \Delta t} \quad(7) \\ p = \frac{m}{m+\mu\Delta t} \quad (8)\]将(7),(8)代入(6),得到方程(2)。说明,阻力谐振子的模型等价于动量梯度递减。如果考虑特殊情况,物体的质量$m=0$,那么此时等价常规梯度递减。
连续情况的稳定性与收敛分析
如果从能量守恒的角度,可以发现损失函数与机械能等价。机械能表示如下
\[E_T = \frac{1}{2}m\frac{dw^T}{dt}\frac{dw}{dt} + E(w) \qquad (9)\]公式(9)中 $\frac{1}{2}m\frac{dw^T}{dt}\frac{dw}{dt}$ 为动能,E(w)为势能。
当振子达到局部最低点的时候,势能为0,动能为0。
在局部最优点$w_0$的地方对受力方程(4)泰勒展开,线性估算得到如下方程,
\[m \frac{d^2 w}{d t^2} + \mu\frac{dw}{dt} \approx -H(w-w_0) \qquad (10)\]其中H为海森矩阵,对称且正定,每个元素为:
\[h_{i,j}= \left. \frac{\partial^2{E(W)}}{\partial (w_i) \partial (w_j)} \right| _{w_0} \qquad(11)\]为了方便计算,且不失去一般性,可以认为$w_0=0$($w_0$为坐标,可以任意定义)。看到正定矩阵,心中一阵狂喜。正定矩阵可以分解,且分解形式非常优美。将H分解如下,其中Q为标准正交矩阵,
\[H = QKQ^T,QQ^T = I \qquad (12)\]K为对称矩阵,且每个元素均大于0, \(K = \begin{bmatrix} k_1\\ & k_2 \\ & & \ddots \\ & & &k_n \end{bmatrix} \qquad (k_i > 0) \qquad(13)\)
可以对w进行线性转换,
\[w^{\prime} = Q^Tw \qquad (14)\]将(12)~(14)代入(10)
\[m \frac{d^2 w^{\prime}}{d t^2} + \mu\frac{dw}{dt} \approx -Kw^{\prime} \qquad (15)\]通过矩阵分解,(15)中的向量每个元素的关系分解开,可以单独考虑,
\[m \frac{d^2 w_i^{\prime}}{d t^2} + \mu\frac{dw_i}{dt} \approx -k_iw_i^{\prime} \qquad(16)\]这里的$k_i$就是弹簧弹性系数。公式(16)是线性微分方程,可以转成矩阵形式求解特征值求解,相关解法可以参考线代随笔15-常系数线性矩阵微分方程。
当不考虑质量时($m=0$),期解为
\[w^{\prime}_i(t) = ce^{\lambda_{i,0}t} \qquad(17)\]其中c为常量,
\[\lambda_{i,0} = -\frac{k_i}{\mu} \qquad (18)\]如果考虑质量($m \ne 0$), 解如下
\[w^{\prime}_i(t) = c_1e^{\lambda_{i,1}t} + c_2e^{\lambda_{i,2}t} \qquad(19)\]其中$c_1,c_2$为常量,
\[\lambda_{i, \begin{Bmatrix} 1\\2 \end{Bmatrix}} = -\frac{\mu}{2m} \pm \sqrt{\frac{\mu}{m}(\frac{\mu}{4m}-\frac{k_i}{\mu})} \qquad (20)\]因为 $\mu>0$且$m>0$,所以 $\lambda_{i, \begin{Bmatrix} 1 \ 2 \end{Bmatrix}} < 0$恒成立,并且很容得到 $|Re \lambda_{i,1} | \le |Re\lambda_{i,2} |$。所以比较两种情况下的收敛速度由 $|Re \lambda_{i,1}|$ 与 $|Re \lambda_{i,0}|$ 决定。
根据论文附录1的推导得到,如果希望动量加快收敛较,即
\[|Re \lambda_{i,1}| > |Re \lambda_{i,0}| \qquad (22)\]那么弹性系数$k_i$必须满足下面条件,
\[k_i \lt \frac{\mu^2}{2m} \qquad(23)\]在最优点附近,$k_i$固定,所以合理设置质量$m 和\mu$,使得大部分方向上述不等式均成立,可以加快整体收敛速度。
定量分析加速的程度,可以令
\[|Re \lambda_{i,1}| = \alpha |Re \lambda_{i,0}| \qquad (24)\]上面两者的解析函数已知,经过变换,可以得到 $\alpha$关于 $k_i$函数,附录2证明了$max(\alpha)=2$,此时$k_i = \frac{\mu^2}{4m}$。此时提高的速度最快。$\alpha$的变化轨迹是,当$k_i$从0到正无穷大变化时, $\alpha$从1到2,然后逐渐减小。当$\alpha < 1$时,此时就无法加速收敛了。可以参考下面的变化示意图,
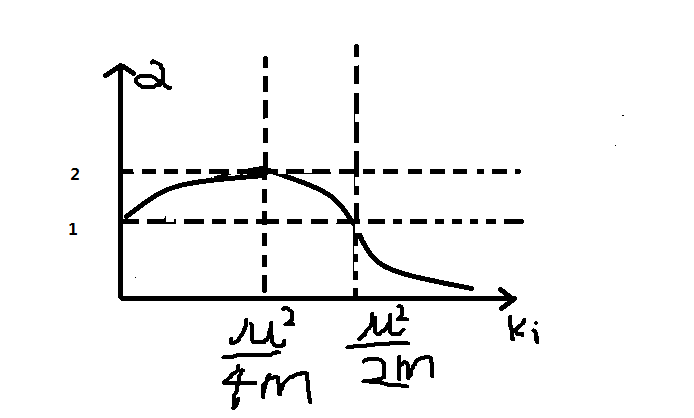
$k_i$的变化,可以概括为三种情况
- $k_i$较小时,阻尼振子几乎没有振动,振幅逐渐减小,缓慢达到稳定平衡,称为过阻尼(Heavy Damping)。
- $k_i$较大时,阻尼振子必须缓慢的经由多次振动逐渐把振幅减小,最后回到平衡位置,因此达成稳定平衡的时间较久,称为欠阻尼(Light Damping)。
- $k_i$在最优点附近时,阻尼振子以最平稳的速度,最短的时间达到稳定平衡,称为临界阻尼(Critical Damping)。
所以,动量加速收敛的根本原因是使得部分特征向量方向的阻力振子到达临界阻尼。
离散情况的稳定性与收敛分析
前面讨论了连续情况的收敛分析,但是计算机是离散的,所以必须验证上面的性质在离散情况下仍然成立,才有意义。
仍然从方程(6)出发,离散情况下,$\Delta t$变为1,仍然在最优点处泰勒展开做线性估算,整理如下
\[w_{t+1} = ((1+p)I-\epsilon H)w_t - pw_{t-1} \qquad (26)\]同样的分解$H$,并且对$w$做线性转换,将方程(12)~(14)代入(26)整理后,
\[w^{\prime}_{t+1} = ((1+p)I-\epsilon K)w^{\prime}_t - pw^{\prime}_{t-1} \qquad (27)\]有$K$是对角矩阵,现在可以分别看待每一个元素
\[w^{\prime}_{i,t+1} = ((1+p)I-\epsilon k_i)w^{\prime}_{i,t} - pw^{\prime}_{i,t-1} \qquad (28)\]方程(28)是一种很常见的迭代方程,可以构建矩阵,使用特征值来求解,
\[\begin{bmatrix} w^{\prime}_{i,t} \\ w^{\prime}_{i,t+1} \end{bmatrix} = A\begin{bmatrix} w^{\prime}_{i,t-1} \\ w^{\prime}_{i,t} \end{bmatrix} = A^t\begin{bmatrix} w^{\prime}_{i,0} \\ w^{\prime}_{i,1} \end{bmatrix} \qquad (29)\]其中$A$根据公式(28)得到
\[A = \begin{bmatrix} 0 & 1 \\ -p & 1+p-\epsilon k_i \end{bmatrix} \qquad(30)\]因为$A^n=S\Lambda^n S^{-1}$,S为特征向量矩阵,$\Lambda$为对角矩阵,对角线为特征值。$w_t$是否收敛,取决于A的特征值,
\[\lambda_{i, \begin{Bmatrix} 1\\2 \end{Bmatrix}}=\frac{1+p-\epsilon k_i \pm \sqrt{(1+p-\epsilon k_i)^2-4p}}{2} \qquad(31)\]如果最后w_t收敛,那么必须特征值的绝对值小于1,
\[\max{(|\lambda_{i,1}|,|\lambda_{i,1}|)} < 1 \qquad(32)\]根据附录3的证明,不等式(32)成立的充分必要条件为
\[\max{(|\lambda_{i,1}|,|\lambda_{i,1}|)} < 1 \Longleftrightarrow -1 \lt p \lt 1 且 0 \lt \epsilon k_i < 2+ 2p\]上面条件所围成的形状正好是一个三角形,如下所示,
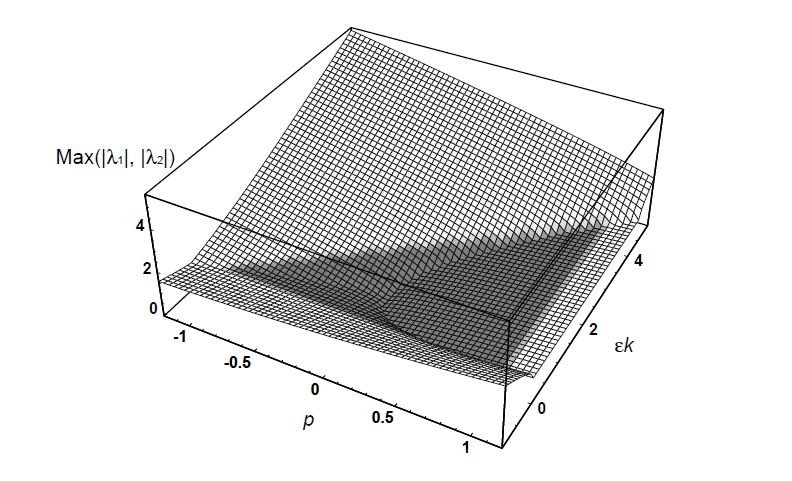
同样的,如果不考虑质量($m=0$),可以得到特征值
\[\lambda_{i,0} = 1-\epsilon k_i \qquad (33)\]只有当 $|\lambda_{i,1}|$ 和 $|\lambda_{i,2}|$ 都小于 $|\lambda_{i,0}|$ 时,动量才会加速收敛。大多数情况下,学习率 $\epsilon$ 非常小,所以为了简化比较,只考虑 $\epsilon \rightarrow 0$的情况下。
公式(31)到公式(34)的变化,仍然是通过泰勒公式的线性估算展开,在 $\epsilon=0$附近的线性估算。
$\lambda_1$关于 $\epsilon$ 的一阶导数以及在 $\epsilon=0$处的值
\[\lambda_{i,1}^{(1)}(\epsilon)=-\frac{k_i}{2}-\frac{k_i}{2}(1+p-\epsilon k_i)\left((1+p-\epsilon k_i)^2-4p\right)^{-\frac{1}{2}} \\ \Rightarrow \lambda_{i,1}^{(1)}(0)=-\frac{k_i}{1-p}\]所以,可以得到 $\lambda_{i,1}^{(1)}$ 在 $\epsilon$ 很小时的线性估算
\[\lambda_{i,1}(\epsilon)\approx \lambda_{i,1}(0) + \lambda_{i,1}^{(1)}(0)\epsilon = 1 - \frac{\epsilon k_i}{1-p}\]同理,得到
\[\lambda_{i,2}( \epsilon ) \approx \lambda_{i,2}(0) + \lambda_{i,2}^{(1)}(0)\epsilon = p(1+\frac{k_i\epsilon}{1-p})\]通过简单的不等式变化,只要 $\epsilon k_i$ 非常小, $0<p < 1-\sqrt{\epsilon k_i}$ 可以确保 $\lambda_{i,1} < \lambda_{i,0}$ 且 $\lambda_{i,2} < \lambda_{i,0}$,也就是确保动量可以提高收敛速度。根据上面p的范围,实践中一般取p为非常接近1的值,比如0.9。同时,由于$0 \lt \epsilon k_i < 2+ 2p$确保收敛,这样也加大了 $\epsilon$ 的取值范围。
总结
本文从阻力谐振子动力模型的角度,定量分析了动量对梯度递减收敛的影响,所有的定量分析都是在最优点附近泰勒展开的线性估算。但是大多数时候,优化起始点可能不是在最优点附近。所以实际上是否可以加快收敛呢?欢迎后续阅读下一篇博文动量加快梯度递减收敛–实践篇,在不同数据集上验证该理论是否可行。
参考资料
您的打赏是对我最大的鼓励!
 支付宝打赏
支付宝打赏
 微信打赏
微信打赏