模拟传播

每个节点可以传播给邻居，但是需要根据传播率$\beta$值判断是否感染。如果当前未感染节点有多个感染的邻居，有机会接受多次交互。传播时间由迭代次数模拟，每一轮迭代需要所有感染节点与邻居交互完毕（交互不一定感染，由感染率决定）。下面是模拟感染的代码：

require(igraph)
require(ggplot2)
require(plyr)

# 每一轮扩散周围邻居
diffuse_neighbour <- function(graph, 
                              index, 
                              tag = 'blue', 
                              beta = 1.0) {
 
  # 保留冗余，冗余的节点被感染机率增加
  nei <- rapply(ego(graph, order=1, nodes = index), 
                function(x) x[-1])
 
  nei_color <- data.frame(
    index = nei,
    color = vertex_attr(graph, index=nei, name ='color'),
    infect = FALSE)
  
  # 计算新增感染者
  for(i in 1:nrow(nei_color)) {
    if(nei_color[i,'color'] != tag) {
      if(runif(1,0,1) < beta) {
        nei_color[i, 'infect'] <- TRUE
      }
    }
  }
  
  new_infect <- unique(nei_color[nei_color$infect,'index'])
  list(graph=set_vertex_attr(graph, name='color', index = new_infect, value = tag),
    vertices = new_infect)
}

# 扩散过程，返回每轮感染的统计数据
diffuse <- function(graph, init_vertices, beta = 1) {
  
  cur_g <- set_vertex_attr(graph, 
                           index = init_vertices, 
                           name='color', 
                           value = 'blue')
  infect_num <- c()
  vertices <- init_vertices
  while(length(vertices) > 0) {
    rst <- diffuse_neighbour(graph=cur_g, index=vertices, tag="blue", beta = beta) 
    cur_g <- rst[['graph']]
    vertices <- rst[['vertices']]
    
    infect <- sum(sapply(vertex_attr(cur_g, name="color"), function(x) x=="blue"))
    infect_num <- c(infect_num, infect)
  }
  
  infect_num
  data.frame(t=1:length(infect_num), infect_num = infect_num)
}

不同感染率对传播的影响

实验采用小世界网络，社交网络中比较常见。随机选取节点作为初始点，使用了高中低三种传播率，每一种感染率计算10轮，计算平均传播曲线。实验代码如下：

set.seed(43545)
round <- 10 # 轮数
beta <- 1 # 感染率
n <- 1500   # 图大小

rst <- data.frame()
for (r in 1:round) {
  g <- sample_smallworld(1, n, 5, 0.05) %>%
     set_vertex_attr("color", value = "red")
  source <- sample(1:n, 1)
  
  for (beta in c(0.2,0.6, 0.9)) {
    rst <- rbind(
      rst,
      cbind(r = r, diffuse(g, source, beta), beta = sprintf("beta=%.2f", beta))
    )
    
    print(sprintf("Round=%d.Beta=%.2f", r, beta))
  }
}

rst_avg <- ddply(rst, .(t,beta), function(x) c(avg_infect_num = mean(x$infect_num)))
p <- ggplot(data=rst_avg, aes(x=t, y=avg_infect_num/n, color = beta))
p <- p + geom_line(size=1.2)
p <- p + guides(color = guide_legend(title = "感染率beta"))
p <- p + scale_x_continuous(breaks=seq(0,50,by=5))
p <- p + scale_y_continuous(breaks=seq(0,1,by=0.1))
p <- p + ggtitle("传播曲线--不同感染率") + xlab("时间(迭代轮数)") + ylab("感染率")
p <- p + theme(legend.text=element_text(size=15),
               text = element_text(size=15))
p

实验结果

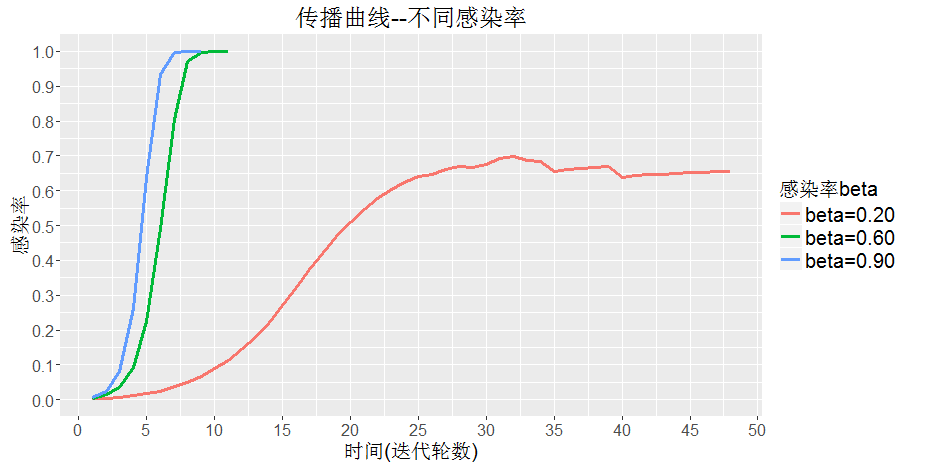
根据实验曲线，可以发现，$\beta$越大，感染越快，这一点与之前的理论一致。但是，如果感染率太低$\beta=0.2$，最后不会感染全部，就会停止传播，这一点传播模型不一致，应该是由于传播模型没有考图的结构，认为所有节点均可以接触到其他节点，所以传播模型最后总可以收敛，只需要多尝试几次。

不同初始点与传播曲线的关系

实验方法与上面类似，仍然采用了20轮，计算平均收敛曲线。不同的是，每一轮均在小世界网络与无标度网络中计算传播曲线，并且根据不同指标，选取了不同的初始点，

最大/最小介数(betweennss)
最大/最小亲密度(closeness)
最大度数
随机

实验代码如下：

set.seed(3456)
round <- 20 # 轮数
beta <- 1 # 感染率
n <- 1500   # 图大小

# 不同点在不同图上的效果
rst <- data.frame()
for (r in 1:round) {
  
  for (g_type in c("small world", "scale free")) {
   
    g <- if (g_type == "small world") {
      sample_smallworld(1, n, 5, 0.05)
    } else {
      sample_pa(n,directed=F)
    }  
    g <- set_vertex_attr(g,"color", value = "red") 
    
    
    # 聚集性与扩散的关系
    cn <- closeness(g)
    rst <- rbind(
      rst,
      cbind(r = r,diffuse(g, which.max(cn), beta), v_type = "max closeness", g_type = g_type),
      cbind(r = r,diffuse(g, which.min(cn), beta), v_type = "min closeness", g_type = g_type)
    )
    
    # 介数传播
    bn <- betweenness(g)
    rst <- rbind(
      rst,
      cbind(r = r, diffuse(g, which.max(bn), beta), v_type = "max betweenness", g_type = g_type),
      cbind(r = r,diffuse(g, which.min(bn), beta), v_type = "min betweenness", g_type = g_type)
    )
    
    # 度
    deg <- degree(g)
    rst <- rbind(
      rst,
      cbind(r = r, diffuse(g, which.max(deg), beta), v_type = "max degree", g_type = g_type)
    )
    
    # 随机
    rst <- rbind(
      rst,
      cbind(r = r, diffuse(g, sample(1:n, 1), beta), v_type = "random", g_type = g_type) 
    )
    
    print(sprintf("Graph Type %s, Round %d Complete", g_type, r))
  }
}
rst_avg <- ddply(rst, .(t,v_type,g_type), function(x) c(avg_infect_num = mean(x$infect_num)))

# 绘图
p <- ggplot(data=rst_avg, aes(x=t, y=avg_infect_num/n, color = v_type))
p <- p + geom_line(size=1.2)
p <- p + facet_wrap(~g_type, nrow=2)
p <- p + guides(color = guide_legend(title = "初始点类型"))
p <- p + scale_x_continuous(breaks=seq(0,50,by=5))
p <- p + scale_y_continuous(breaks=seq(0,1,by=0.1))
p <- p + theme(legend.text=element_text(size=15),
               text = element_text(size=15))
p <- p + ggtitle("传播曲线--不同初始点") + xlab("时间(迭代轮数)") + ylab("感染率")
p

实验结果

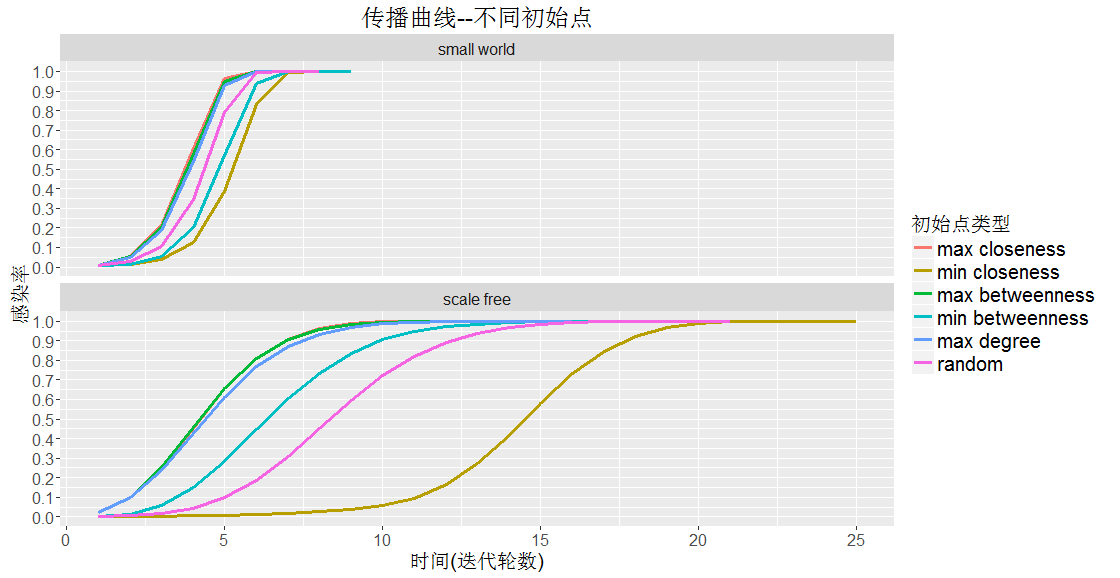
根据实验结果，整体而言，小世界网络(small world)的收敛明显快于无标度网络(scale free)，可能是由于小世界网络聚集程度比较均匀，传播概率高，而无标度图聚集度过于集中在某几个点，导致传播概率低。

小世界网络 高介数，高亲密度，高度数的传播速率差异不大，随机节点中游，低介数高于低亲密度。
无标度网络 高介数与高亲密度的传播速率基本一致，但是最小介数的传播熟虑竟然快于随机点。

结论

根据上面的试验，对图的传播率有了感性认识，希望对后面工作有知道意义，实验结论总结如下:

在传播率较高的情况下，传播曲线与理论吻合比较好，呈现明显S形状，并且收敛
在传播率较低时，传播曲线不能收敛
小世界网络的传播速率明显高于无标度图
高介数，高亲密度和高度数的传播速率在小世界网络区别不明显，但是收敛较快，考虑到介数与亲密度的计算量，使用高度数作为初始点，更为经济实惠。