网络传播-理论篇

最近看了一些网络传播扩展方面的内容，总结了网络扩散的数学理论以及相关实验。本博文主要介绍网络扩散的数学模型，下篇记录相关实验。

先定义一些符号，

n=总人数
I=已经扩散的人数
$i=\frac{I}{n}$ 扩散占比
S=还没哟扩散的人数
$s=\frac{S}{n}$ 未扩散的占比
$\beta$ 感染率

根据定义，容易得到 $S+I=n,s+i=1$ 。

扩散模型可以微分方程表示，如下

\frac{d I}{d t} = β S \frac{I}{n}

$\frac{dI}{dt} = \beta S \frac{I}{n}$

扩散速率等于没有感染的人群遇到感染人群的概率并乘以感染率。将人数转成感染率，并且去掉S，可得到下面的微分方程

\frac{d i}{d t} + β i^{2} - β i = 0 (1)

$\frac{di}{dt} + \beta i^2 - \beta i = 0 \quad (1)$

上面是一阶非线性微分方法，想办法转成线性微分方程才有办法解决，设 $y=\frac{1}{i} \quad (2)$ ，将(2)代入(1)整理如下,

\frac{d y}{d t} + β y = β (3)

$\frac{dy}{dt} + \beta y = \beta \quad (3)$

现在是一阶非齐次线性微分方程，根据变系数线性微分方程通解，可以得到下面的关于y的方程

y = 1 + (C_{1} + C_{2} β) e^{- β t} (4)

$y=1+(C_1+C_2\beta)e^{-\beta t} \quad (4)$

将(4)代入(2),得到关于感染率 $i$ 的方程,

i = \frac{1}{1 + (C_{1} + C_{2} β) e^{- β t}} (5)

$i = \frac{1}{1+(C_1+C_2\beta)e^{-\beta t}} \quad (5)$

(5)式中， $C_1,C_2$ 是常量， $t$ 是时间，形状是个S，类似sigmoid函数，其中 $\beta$ 控制收敛速率， $C_1,C_2$ 控制偏移，扩散曲线如下，第一组参数是sigmoid函数：

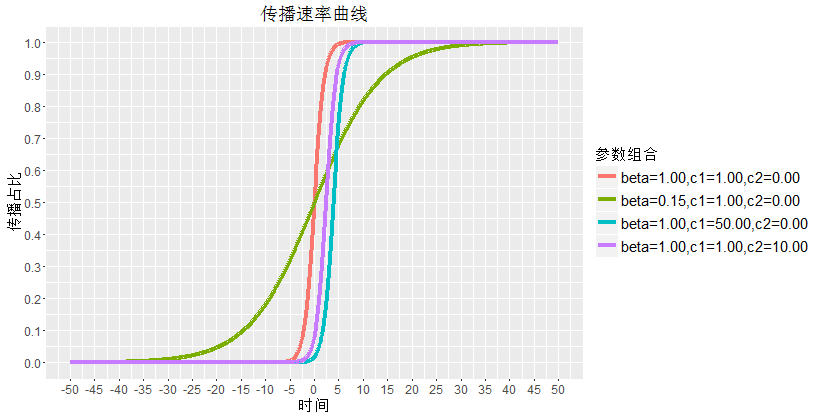
在上面的推导过程中，没有用到网络的任何特性，好像与网络没有什么关系。下一篇博文中，将会探讨网络中传播率与上面曲线的关系。

曲线生成代码(R语言)

require(ggplot2)

# 传播率函数
i <- function(t, beta, c_1, c_2) {
  1 / (1 + (c_1 + c_2*beta)*exp(-beta*t))
}

# 曲线生成函数
curve_date <- function(t_seq, beta, c_1, c_2) {
  
  i_seq <- sapply(t_seq, i, beta, c_1, c_2)
  param <- sprintf("beta=%.2f,c1=%.2f,c2=%.2f", beta, c_1, c_2)
  data.frame(time=t_seq, rate=i_seq, type=param)
}

# 时间范围
t_seq <- seq(-50, 50, by=0.1)

# 生成数据
rst <- rbind(
  curve_date(t_seq, beta = 1, c_1 = 1, c_2 = 0),
  curve_date(t_seq, beta = 0.15, c_1 = 1, c_2 = 0),
  curve_date(t_seq, beta = 1, c_1 = 50, c_2 = 0),
  curve_date(t_seq, beta = 1, c_1 = 1, c_2 = 10)
)

# 绘图
p <- ggplot(rst, aes(x=time, y=rate, color = type))
p <- p + geom_line(size=1.5)
p <- p + guides(color = guide_legend(title = "参数组合"))
p <- p + ggtitle("传播速率曲线") + xlab("时间") + ylab("传播占比")
p <- p + scale_x_continuous(breaks=seq(min(t_seq),max(t_seq), by = 5))
p <- p + scale_y_continuous(breaks=seq(0,1, by = 0.1))
p <- p + theme(legend.text=element_text(size=15),
               text = element_text(size=15))
p