强化学习笔记09-利用与探索
这一讲的问题很有意思—-利用与探索,有点类似哲学问题。举个例子,比如牛排的酱汁,你会选择一个没有吃过的酱汁,还是选择经典黑椒汁。在这个问题上,我和我老婆总是不一致。她总是坚定的选择黑椒汁(Exploitation),而我每次都想尝试新的酱汁(Exploration),不过最后不得不承认黑椒汁味道最好。可以看出探索是有代价的,这个例子里面探索的代价较大,比不上带来的收益。换个例子,比如近代欧洲的大航海时代,葡萄牙,西班牙,英国,荷兰这些本土面积较小的国家,正是通过探索,找到了比自己本国大得多的殖民地,并且带来了巨大的财富。探索有利有弊,关键是否根据自身情况合理使用。
回想一下强化学习的环境下,哪个地方需要对利用和探索之间做出权衡?前面多次提到的$\epsilon-$greedy的策略就是利用与探索的例子。这是一个非常navie的方法。本讲后面会讨论其他设计更加精细的利用和探索策略。但是,介绍此方法时不宜在强化学习环境下探讨,因为太多不相关的东西,容易分散注意力。一般都简化为多臂老虎机问题上探讨这类问题。
问题定义
假设有10个老虎机,每个老虎机中奖的概率分布不同(如下图),如果在有限的选择下找到最好的那个老虎机,这就是多臂老虎机问题,
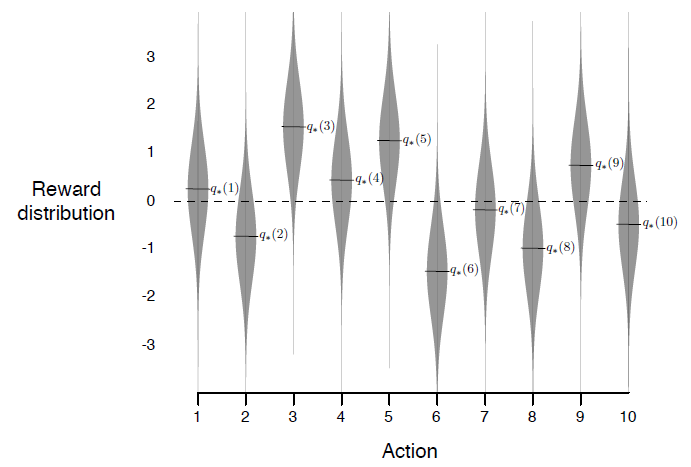
可以看到,10个老虎机,有5个的收益是正数,5个是负数。那么如果准确快速的找到那些收益正的老虎机?定义动作值函数
\[q(a) = E[R_t|A_t = a]\]其含义是动作为a的期望收益。上面的例子中,如果a=3,那么$q(3)=1.5$。我们不是先知,这个值无法得到,但是可以通过统计的方法估算出来,
\[Q_t(a) = \frac{\sum_{i=1}^{t-1}R_i I(A_i = a)}{\sum_{i=1}^{t-1} I(A_i = a)}\]所以,经过很多步后,我们可以估算出每个动作a的值,然后选择用贪心策略,
\[A_t = \arg_a \max Q_t(a)\]得到最优的动作a。理论上,上面的方法一定能够找到最优动作,但是实际情况是我们没有那么多赌资去计算出所有的$Q(a)$。所以,后面的所有方法都是如何在较短的资源(动作)下,快速找到最优动作,使得总体收益快熟收敛到最优。
$\epsilon-Greedy$老虎机算法
算法伪代码如下,核心思想就是每次选择时,留下$\epsilon$的概率随机选择动作(Exploitation),剩下的$1-\epsilon$概率用贪心策略选择动作(Exploration)。
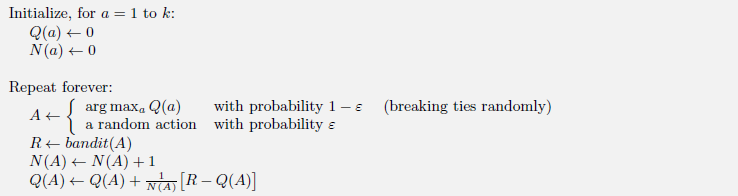
更新规则可以总结为
\[NewEstimate \leftarrow OldEstimate + StepSize[Target - OldEstimate]\]此规则在后面会反复提到。其意义是每次更新,都是朝目标target进行小小的一步。StepSize在上面的例子是$\frac{1}{n}$,不过更为通用的形式为$\alpha_t(a)$。
处理非静态(Nonstational)分布问题
前面提到的算法可以处理静态分布的问题,即每个老虎机的奖励分布是不变的。但是大多数情况新,需要处理非静态分布问题,尤其是在强化学习问题中。在此情况下,一般需要将近期的奖励的权重放大,而不是像上面那样近期的奖励的权重会越来越小。比较常用的做法是将StepSize设置为常量$\alpha$。那么更新策略跟改为
\[Q_{n+1} = Q_n + \alpha[R_n - Q_n]\]其中$\alpha \in (0,1] $。将此公式递归展开
\[\begin{align} Q_{n+1} &= \alpha R_n + (1-\alpha)Q_n \\ &= \alpha R_n + (1-\alpha)(\alpha R_{n-1} + (1-\alpha)Q_{n-1}) \\ &= \alpha R_n + \alpha(1-\alpha)R_{n-1} + (1-\alpha)^2 Q_{n-1} \\ &= \alpha R_n + \alpha(1-\alpha)R_{n-1} + \alpha(1-\alpha)^2 R_{n-2} + (1-\alpha)^3 Q_{n-2} \\ &= (1-\alpha)^n Q_1 + \sum_{i=1}^n \alpha(1-\alpha)^{n-i}R_i \qquad (1) \end{align}\]展开式非常有特点,$Q_1$与$R_i$的系数之和为1,且均大于等于0,即$(1-\alpha)^n+ \sum_{i=1}^n \alpha(1-\alpha)^{n-i}=1$,可以认为$Q_{n+1}$是$Q_1$与$R_i$的加权平均值。如果更为通用一点,可以将$a_n(a)=a$代入上面的公式,
\[Q_{n+1} = (1-\alpha_n(a))^n Q_1 + \sum_{i=1}^n \alpha_i(a) (1-\alpha_i(a))^{n-i}R_i\]即学习率随着步长和行为变化,一个著名的随机逼近理论证明如果$\alpha_n(a)$满足下面条件,那么$Q_{n+1}$收敛。
\[\sum_{n=1}^\infty \alpha_n(a) = \infty \qquad and \qquad \sum_{n=1}^\infty \alpha_n^2(a) < \infty\]如果$\alpha_n(a) = \frac{1}{n}$,即平均值,那么满足上面条件,最后会收敛。如果$\alpha_n(a) = a$为常量,不满足第二个条件,所以不会收敛。虽然不收敛,但是对于Nonstational的环境下,确实需要这种特性才能捕捉到最优的策略。
优化初始值
初始值的优化可以鼓励探索,因为重上面的公式(1)可以发现初始值对最后的收益和有一定的影响的。我们可以通过先验知识设定初始值,比如如果老虎机的收益最高不操过1,那么我们可以认为的设定所有的老虎机的初始值都是5,这样必然导致每个老虎机都不太好,从而算法会尝试所有的老虎机,等价于探索过程。当然,这也增加了我们设置初始值的工作。不过,此方法对Nonstational的环境效果不好,因为初始值的作用效果不会一直存在,随之步数的增加,作用会越来越小。下面看看初始值的实现腰果,
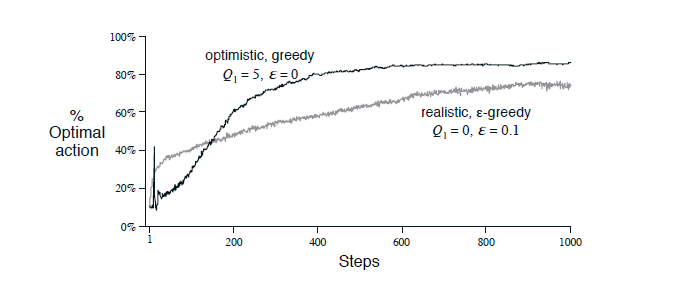
优化的初始值虽然开始很慢,但是由于强制尝试了很多,后面的收敛速率就明显比$\epsilon-greedy$快。
Upper Confidence Bound动作选择
此方法根据Hoeffding不等式推导出来,用于估计每个Q(a)上界, \(A_t = \arg_a \max \left[Q_t(a) + c\sqrt{\frac{\ln t}{N_t(a)}} \right]\) 其中$N_t(a)$表示执行t次中,选择动作a的次数,$t$表示总的次数。直观上解释,就是$a$执行的越多,那么就越能够确定a的上界,$a$的整体值的估计就越真实;如果$a$执行的越少,那么a的上界越大,也就会越多的选择a,类似一种探索过程。$c$是一个常量,用于控制探索的粒度,$c$越大,探索越频繁。UCB也常用于MCTS过程中。
梯度老虎机算法
使用一种倾向性指标$H(a)$作为选择a的权重,权重用soft-max计算出概率。$H(a)$的绝对值没有意义,只是他们的相对值可以计算出选择a的概率。H(a)的更新算法如下
\[H_{t+1}(A_t) = H_t(A_t) + \alpha(R_t - \bar{R})(1-\pi(A_t)) \ and \\ H_{t+1}(a) = H_t(a) - \alpha(R_t - \bar{R})\pi(a) \ for \ all \ a \ne A_t\]$\bar{R}$是收益均值,可以用增量方法计算。如果当前动作$A_t$收益大于均值,那么就会增加再次选择$A_t$的概率,否则会降低其概率。此算法的更新方式,本质上是随机梯度递增(SGA),具体推导可以参考Sutton教材(2017)2.8节。
总结
到目前为止,介绍了4种多臂老虎机问题,但是这里面忽略了状态,如果考虑状态那就是马尔科夫决策过程(MDP)问题,可以利用之前学习到的技术解决。虽然教材和讲义中大多以$\epsilon-greedy$作为动作选择策略,但是上面提到的算法等价,可以相互替换其在强化学习中使用。
您的打赏是对我最大的鼓励!
 支付宝打赏
支付宝打赏
 微信打赏
微信打赏