最近在准备组内强化学习第5,6讲的分享，顺便回顾了前面的所有内容，所以这篇笔记姗姗来迟。本章的内容是介绍Planning，以及将Learning与Planning结合起来技术。前面的课程中谈到过Planning，即Dynamic Programming。Planning就是在已知Model的情况下计算最优的策略。Planning需要先要根据经验得到模型，大致形式如下

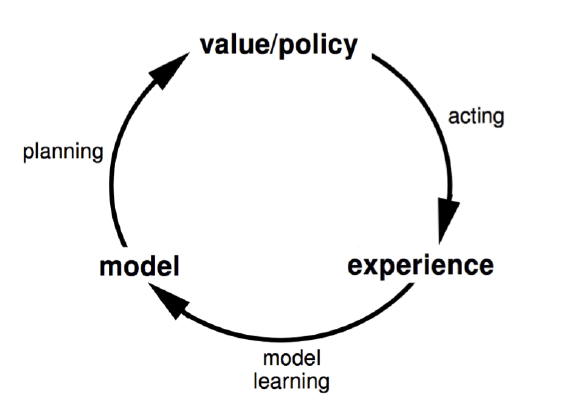
在强化学习领域内，模型就是P（转移概率）和R（奖励），所以模型就是根据状态S和动作A，估计出对应的P与R。这个是不是在哪里遇到过？没错，这个就是监督学习。定义模型为$M=\langle P,R \rangle$，最后求解下面的形式

\(S_{t+1} \sim P_\eta(S_{t+1} \vert S_t, A_t) \\ R_{t+1} = R_\eta(R_{t+1} | S_t,A_t)\) 一般假设状态转移和奖励相互独立。

既然是监督学习，那么就可以使用监督学习中的那些方法求解。当有模型后，可以用之前的动态规划方法求解最优策略。除此之外，还可以利用之前提到的Model Free的方法求解最优策略，把模型当做环境，不断生成样本，那么就是无缝使用MC-Control，SARSA和QLearning等方法。

但是模型一定有误差，基于有误差的模型，学习到的策略也不是最优的。所以，比较好的方法是集成Planning和Learning两个过程，model和policy一起学习，相互促进，而不是完全要Model引导Policy。这类方法称为Dyna,流程大体如下

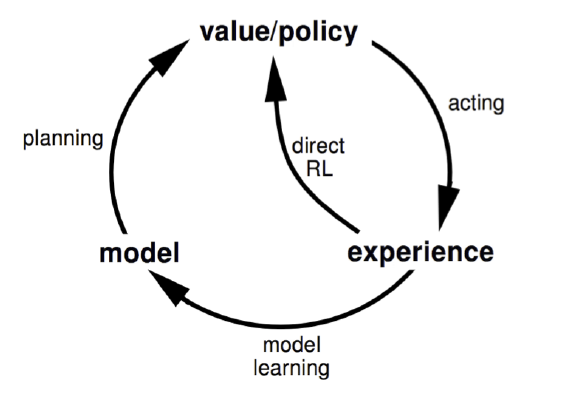
在原始Planing的方法下，整合了Model Free的学习方法。最为基础的算法是Dyna-Q，其伪代码如下

当$n=0$时，Dyna-Q就退化成了Q-Learning。经过一些实验，可以看到Dyna-Q收敛速率比Q-Learing要快很多，因为一旦有了模型，可以自己生成样本自己学习，而不需要与环境交互，有点类似左右互搏的效果。

最后介绍MCTS: Monte Carlo Tree Search。该方法的核心思想就是采样。MCTS通过采样的方法，扩展树的结构，并且不断评估候选状态的值函数。在状态空间特备复杂的情况下，比如围棋。如果每次从起点开始模型，那么效率会非常低。MCTS使用启发式方法，每次在当前一个较好的状态下继续探索，探索方法即使随机样本，直到得到最优的方案。MCTS由于在AlphaGo中应用，被广为人知，下面这张动图可以形象解释MCTS的工作源里，

蒙特卡洛树是什么算法？ - fly qq的回答 - 知乎比较容易理解。更为学术资料，可以参考mcts.ai。

分享总结 2018-1-22

本次风向中，谈到了Dyna为什么会比非Dyna收敛快。因为在Dyna中，有个内部simulate，在此过程中，S和A是随机取的，可以尝试一些情况，而这些情况在与真实环境交互时，无法得到。同时，自我交互的过程相当于自己模拟，可以减少真实的交互次数，即减少step次数。

谈到了MCTS，该技术06年发明，后来很多围棋AI都是基于MCTS的优化和改进，最好的一个是日本开发的Zen，但是均没有达到人类冠军的段位，直到AlphaGo的出现，它在MCTS的基础上，融合了深度学习和强化学习，打败了人类冠军。

MCTS在探索的时候，起点是Current State，然后使用Tree Policy只搜索$d$层,$d$层以后的就用随机模拟和其他模拟方法快速的模拟，得到结果，然后更新到根节点。经过k轮后，从当前状态，找到一个最优的action进行扩展，然后继续这个循环。深度学习应用在d层以后，可以直接通过监督学习算出来，而不是模拟出来。如果不用深度学习，在最开始会比较弱，深度学习弥补了开始时比较弱的情况。