强化学习笔记05-无模型(Model Free)策略求解
这一讲合并了Sutton教材5,6,7章的后半部分。上一讲主要介绍MC,TD的值函数计算。即给定policy,估计值函数$V(s)$。这一讲,介绍求解最优policy,大概内容如下:
- MC $\epsilon$-贪心求解策略
- SARSA: TD On-Policy $\epsilon$贪心求解策略
- Q-Learning: TD Off-Policy $\epsilon$贪心求解策略
On/Off-Policy的区别
- On-Policy学习:直接通过目标策略$\pi$采样,学习目标策略$\pi$
- Off-Policy学习:通过行为策略$\mu$采样,学习目标策略$\pi$
On-Policy是Off-Policy的一个特例,目标策略和行为策略一致。Off-Policy可以通过其他更优策略,解决当前问题,比如学习人类专家的行为,更为灵活。
$\epsilon-$贪心探索
核心思想是让m个行为均有机会得到尝试,而不是总是尝试当前最优的行为。设置参数$\epsilon \in [0,1]$,以概率$1-\epsilon$使用最优行为(即贪心),或以概率$\epsilon$随机选择一个行为,形式的表示如下
\[\begin{equation} \pi(a\vert s)=\left\{ \begin{array}{@{}ll@{}} \epsilon/m + 1-\epsilon & \text{if}\ a^*=\arg \max_{a \in A(S)} Q(s,a) \\ \epsilon/m & \text{otherwise} \end{array}\right. \end{equation}\]根据上面定义,可以发现$\sum_{a \in A(s)} \pi(a \vert s) = 1$ 。$\epsilon$-贪心策略可以通过调整探索的系数$\epsilon$ ,控制探索范围,可以更好的在Exploitation和Exploration上权衡。
加权平均小于等于最大值
后面证明$\epsilon$-贪心策略可以确保策略更新时会用到加权平均小于等于最大值。假设数组$X={x_1,x_2,\cdots, x_n}, \ x_i \in R$,证明
\[\max(X) \ge \sum_{i=1}^n w_ix_i \qquad (1) \\ s.t. w_i \ge 0 且 \sum_{i=1}^n w_i = 1\]对$w_i$进行通分,转成如下形式
\[w_i = \frac{m_i}{M} \qquad (2) \\ s.t. \sum_{i=1}^n m_i = M, M \gt 0, m_i >= 0\]任意小数是可以转成分数形式,不断通分,可得到(2)。将(2)代入(1),
\[\max(X) \ge \sum_{i=1}^n \frac{m_i}{M}x_i \\ \Leftrightarrow M \max(X) \ge \sum_{i=1}^n m_ix_i \qquad (3)\](3)不等式的左边有M个最大值,右边有m个值,但是他们都小于等于$max(X)$,所以(3)不等式恒成立,证毕。
$\epsilon-$贪心策略提升
贪心策略是可以稳定提升值函数值,
\[\begin{align} q_\pi(s, \pi^{\prime}(s)) &= \sum_{a \in A(s)} \pi^{\prime}(a \vert s) q_\pi(s,a) \qquad Line \ 1\\ &= \epsilon/m \sum_{a \in A(s)}q_\pi(s,a) + (1-\epsilon) \max_{a \in A(s)} q_\pi(s,a) \qquad Line \ 2 \\ &\ge \epsilon/m \sum_{a \in A(s)}q_\pi(s,a) + (1-\epsilon) \sum_{a \in A(s)} \frac{\pi(a \vert s) - \epsilon/m}{1-\epsilon} q_\pi (s,a) \qquad Line \ 3 \\ &= \sum_{a \in A(s)} \pi(a \vert s) q_\pi(s,a) = v_\pi(s) \qquad Line \ 4\\ \end{align}\]第二行是根据$\epsilon-$贪心策略定义得到,第三行中$ \sum_{a \in A(s)} \frac{\pi(a \vert s) - \epsilon/m}{1-\epsilon} = 1$,所以该项是加权平均数系数。第二行到第三行使用了上面证明的定理。后面的证明顺水推舟。证明的关键是构造这个加权平均的系数,非常漂亮。
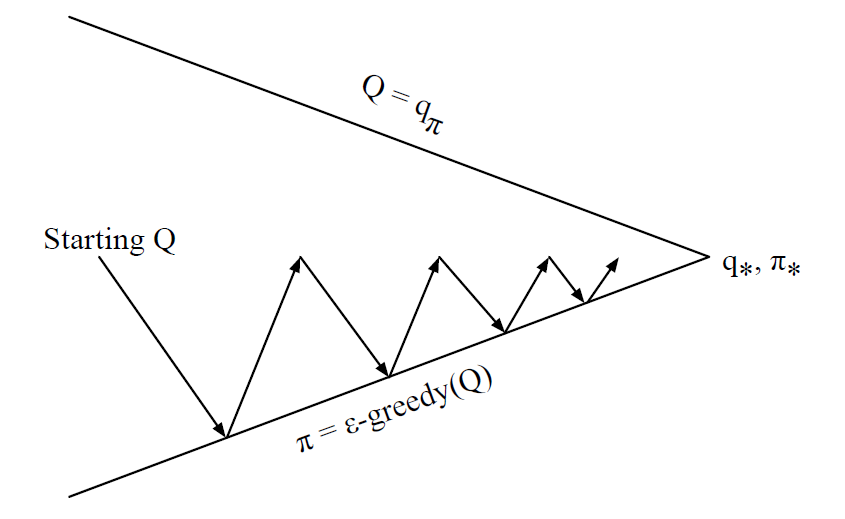
基于$\epsilon$-Greedy策略的Monte-Carlo控制
具体实现代码和实验效果参考参考这里。MC控制中的Policy评估时以单个Episode为单位更新,而不是纯MC Evaluation那样一次性使用多个Episode。主要是为了提高计算效率,与SGD用来提高GD的效率,有异曲同工的效果。所以示意图只绘制了一半,
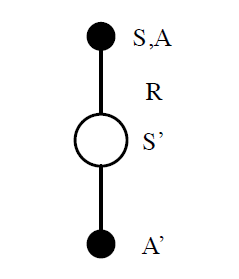
SARSA
目标数值使用TD(0)替换MC,就是SARSA算法。由于更新需要5个样本序列$S_t,A_t,R_t,S_{t+1},A_{t+1}$,所以简称SARSA。相比于MC版本,SARSA效率更高,可以在线更新,无需等待Episode结束,方差更低。
更新公式
\[Q(S,A) \leftarrow Q(S,A) + \alpha(R + \gamma Q(S^\prime, A^\prime) - Q(S,A))\]为什么说是TD(0)?因为只看了后面一步既可以更新Q函数。为什么是On-Policy?因为完全通过策略$\pi$的样本,没有使用其他策略样本。SARSA算法伪代码如下,

前面提到过,sarsa效率会比MC Control高,在Windy Grid World实验中,SARSA只用了50轮就收敛了;而同样时间内,MC甚至无法完成一轮完整采样。
Sarsa可以通用化扩展为$Sarsa(\lambda)$,目标使用$TD(\lambda)$替换$TD(0)$,先定义$q^{(n)}_t$和$q_t^{\lambda}$,然后使用后向视角逐步更新,具体细节这里略去,详情可以参考教材和幻灯片对应章节。
Q-learning
在讲具体算法之前,需要先了解Importance Sampling,主要思想是用已知的分布p,去估算未知或复杂的分布q的特性的方法,比如q的期望,方差,概率积分等。为什么Q-Learning是Off-Policy ,因为它用行为$\epsilon$-贪心策略去更新目标贪心策略,其更新图如下,
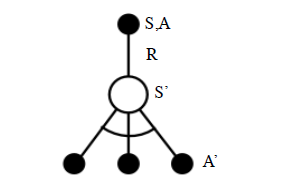
其中,S,A,R是根据$\epsilon$贪心策略生成,$S^\prime,A^\prime$用来更新贪心策略。更新公式
\[Q(S,A) \leftarrow Q(S,A) + \alpha(R+\gamma \max_{a^\prime}Q(S^\prime,a^\prime) - Q(S,A))\]算法伪代码,
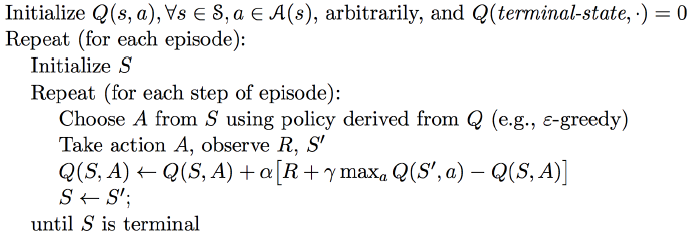
虽然重要性采样可以应用到off-policy的强化学习算法中,但不一定必须使用。Q-Learning就没有使用重要性采样,而是直接使用贪心策略获取目标Q值。使用强化学习笔记-Talk is cheap, show me the code提到的Cliff实验显示,Q-Learning的收敛速率的确比Sarsa(0)要快,而且也更为稳定,具体实验数据,可以参考这里。下面是网络上找到的sarsa与Q-learning在Cliff walk例子上的示意图。
SARSA
Q-Learning
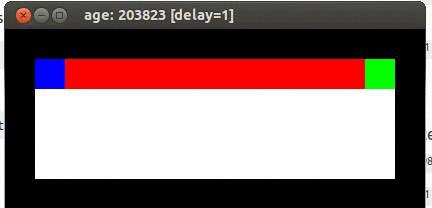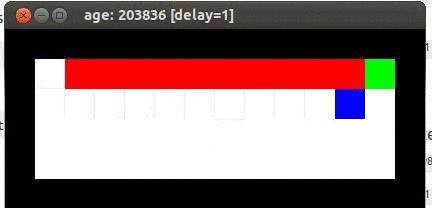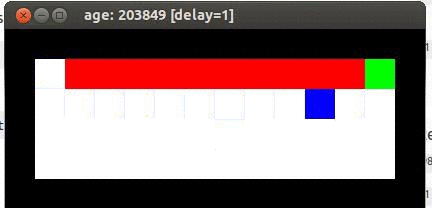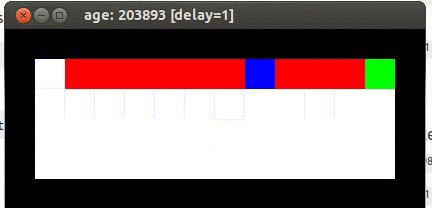
最优的算法是贴着悬崖走,但是这会导致偶尔摔下悬崖,Q-Learning学习到了这一点。SARSA学习到一个更安全的方法,虽然不是最优,但是更稳妥。
动态规划DP与时分TD的比较
为什么没有提到MC,MC是$TD(1)$,所以不单独拿出来。下面是更新图和更新方法的区别,作为总结。
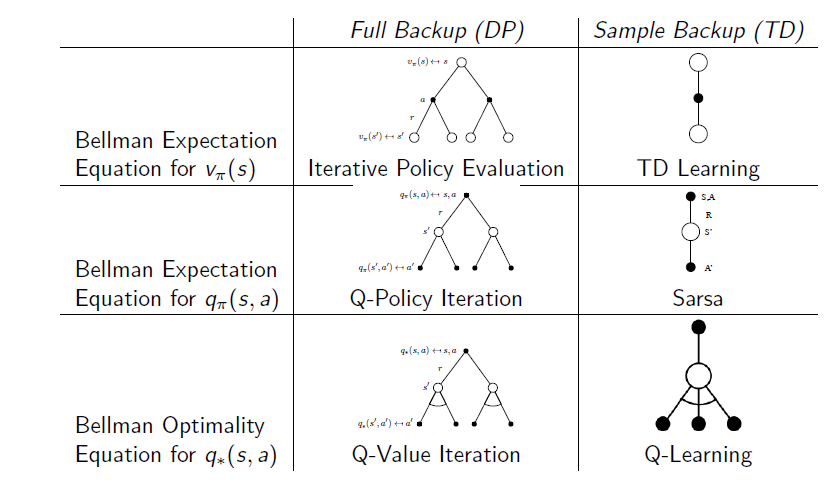
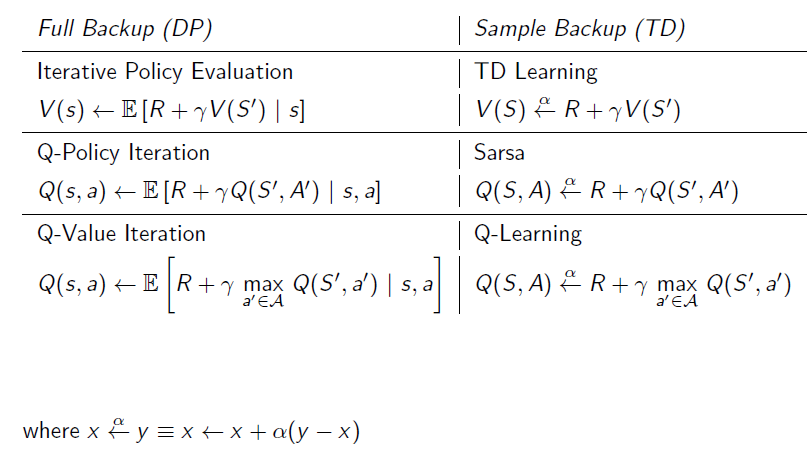
目前,我们处理的问题都是离散的,即Q的状态空间是十分有限的,如果遇到状态空间是连续的,或者范围很大,怎么办?这也是后面的章节将要处理的问题。
2018年1月2日分享
今天在RL学习小组内分享了本章内容,谈到了为什么Q-Learning没有使用重要性采样。这里有个历史原因,重要性采样是有很好的数学特性的,在off-policy最开始的研究中,引入了重要性采样,但是重要性采样计算比较复杂。后来发现其实不用重要性采样,也可以做off-policy学习,比如Q-Learning,其实Q-Learning对比DP求解最优解的采样形式,可以参考倒数第二页DP与TD的比较。
风墙例子中,Monte-Carlo控制连一轮都无法完成,因为完全随机的初始策略,根本无法完成一轮,那股风太强劲。这引出了一个更一般的问题,在特别复杂的系统中,完全随机的初始策略可能不是一个好的选择,可能导致永远不能收敛。可行的方法是通过先验知识获得一个初始策略,比如通过监督学习的方法获取初始策略。
您的打赏是对我最大的鼓励!
 支付宝打赏
支付宝打赏
 微信打赏
微信打赏