强化学习笔记03-动态规划
动态规划与MDP的关系
动态规划是一种叫常见的求解最优解算法,一般问题具符合以下两个特性,可以使用动态规划求解
- 问题可以迭代表示,即问题可以分解为子问题
- 子问题可以被缓存和复用
MDP符合上面的特点
- Bellman公式是迭代形式,也就是可以用子问题表示
- 可以存储和复用值函数,
虽然动态规划可以解决MDP问题,但是需要知道的内容太多,基本上要知道MDP的所有参数,$<S,A,P,R,\gamma>$,实际问题中很难实现。所以虽然动态规划的思路无法直接应用到实际问题,但是后续改进方法都是基于动态规划的思路,所以还是非常有必要了解如和使用动态规划求解MDP问题。
策略评估 Policy Evaluation
给定一个策略,计算出所的值函数$v(s)$。同步的方法,步骤如下
- 在每次迭代k+1
- 对所有的状态$s \in S$
- 使用$v_k(s\prime)$更新$v_{k+1}(s)$
- $s^{\prime}$是$s$的后续状态
经过一段迭代后,该值会收敛,状态值会逐步变化,最后收敛到$v_\pi$,如下
\[v_1 \rightarrow v_2 \rightarrow \cdots \rightarrow v_\pi\]注意!根据实验,即使$\pi$固定,最终的$v_\pi$依赖$v_1$的值。
Backup Diagram形象的描述整个更新过程,
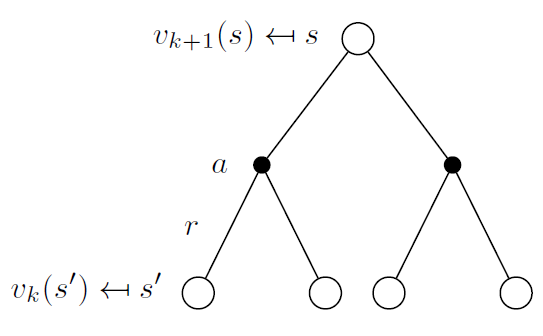
在状态$s_{k+1}$,可以选取不同动作$a$,并且有即时回报$R_s^a$。通过类似广度搜索的方式,遍历所有动作,数学形式如下,
\[v_{k+1}(s)=\sum_{a \in A }\pi(a \vert s)\left(R_s^a + \gamma\sum_{s^{\prime} \in S} P_{ss^{\prime}}^av_k(s^{\prime}) \right) \\ v^{k+1} = R^\pi + \gamma P^\pi v^k \qquad 矩阵表示\]可以将$v_{k+1}$变形一下,将$\sum$提取到最左边,方便编程实现,变化如下
\[\begin{align} v_{k+1}(s) &=\sum_{a \in A }\pi(a \vert s)\left(R_s^a \sum_{s^\prime \in S} P_{ss^\prime}^a + \gamma\sum_{s^{\prime} \in S} P_{ss^{\prime}}^av_k(s^{\prime}) \right) \\ &=\sum_{a \in A }\pi(a \vert s)\left( \sum_{s^\prime \in S} P_{ss^\prime}^a R_s^a + \sum_{s^{\prime} \in S} \gamma P_{ss^{\prime}}^av_k(s^{\prime}) \right) \\ &= \sum_{a \in A } \sum_{s^\prime \in S} \pi(a \vert s) P_{ss^{\prime}}^a \left( R_s^a + \gamma v_k(s^{\prime}) \right) \\ \end{align}\]具体的编程实现,参考这里。
策略改进 Policy Improvement
前面讲过,策略的优劣,是由对应的值函数反映,
\[\pi^{\prime} \ge \pi, if \ v_{\pi^\prime}(s) \ge v_{\pi}(s),\forall s \in S\]使用朴素的贪心思想,得到更有的策略$\pi^\prime$。对于确定性的策略,即$\pi(a \vert s)=1$,有$v_{\pi}(s) = q_{\pi}(s,a)$。使用贪心策略,
\[\pi^\prime(s)=\arg \max_a q(s,a)\]这样,只需要一步,就可以完全确保新的值函数不比之前的值函数差,
\[v_{\pi^\prime}(s)=q(s, \pi^\prime(s)) = \max_a q_\pi(a,s) \ge q_\pi(a,s) = v_\pi(s)\]最后一定会收敛,因为存在最优解,那么一定有上界,所以迭代一点点在变好,那么一定会达到最优解。可以通过下面的示例图形象的刻画整个过程。
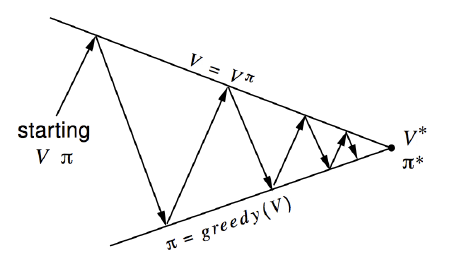
结合策略评估和策略改进的过程,求解最优策略和最优值函数的方法称为策略迭代。值迭代最终收敛的策略和值函数,与初始值函数也是强相关的,具体可以参考算法实现以及实验数据。如果使用贪心策略,最终获取的策略是决定性的,而不是概率论分布。
值迭代 Value Iteration
常用算法图最短路径-Dijkstra算法,就是一种值迭代方法。最终的最短路径,是通过前一个最短路径中,通过贪心策略选取当前最短路径找到。 其计算方法如下
- 在迭代k+1过程
- 所有状态$s \in S$
- 直接使用$v_k(s^{\prime}) $更新$v_{k+1}(s)$
相比于策略迭代,值迭代直接在原来的状态上收敛更快,存储要求更少,数学形式如下
\[v_{k+1}(s) = \max_{a \in A} R_s^a + \gamma \sum_{s^\prime \in S} P_{ss^\prime}^a v_k(s^\prime) \\ v_{k+1} = \max_{a \in A} R^a + \gamma P^av_k\]在得到最优解后,最优策略可以直接根据贪心的方法得到。此算法与策略评估比较类似,不同在于更新值时,使用贪心策略,而不是获取期望。同样,与Policy Evulation和Policy Improvement类似,Value Iteration的最终值与初始状态有关,可以参考算法实现和实验。
总结前面三个算法,
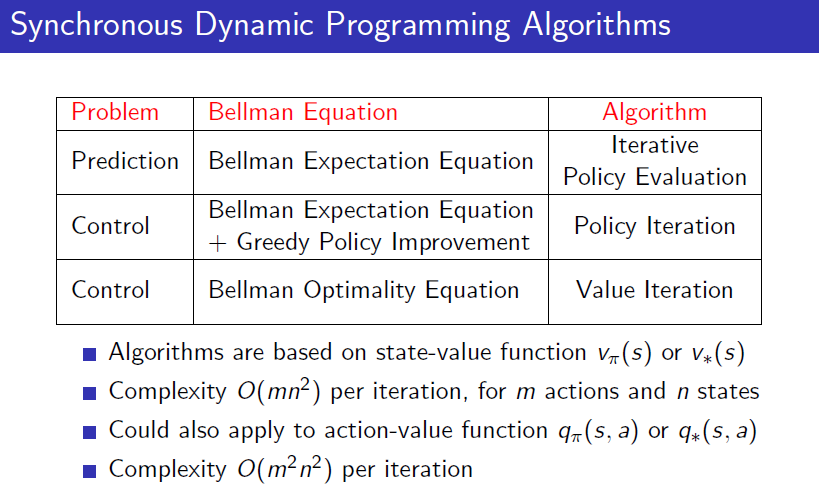
您的打赏是对我最大的鼓励!
 支付宝打赏
支付宝打赏
 微信打赏
微信打赏