参数选择在LSH中非常重要，直接影响计算性能和准确率。利用上篇博文的理论，现在可以轻易解决参数设定的问题。本文通过一个简单的例子，描述如何选择参数，并且提供参考代码。

选取w

首先，假设数据源D的每行数据$x\in R^{100}, 0 \le x_i \le 1$。说明最大的距离是$10(=\underbrace{\sqrt{1+1+\cdots+1}}_{100})$。可以认为$r_1=0.5$是一个比较近的范围，$r_2=9.5$是一个比较远的范围。希望lsh可以在大于等于0.75的概率使在$r_1(= 0.5)$内的数据投射到一起，同时小于等于0.05的概率使相距$r_2$以外的数据不投射到一起。使用下面代码，看看相关概率：

# 碰撞函数
root_fun <- function(target) {
  function(c) {
    1-2*pnorm(-1/c) + (2*c/sqrt(2*pi))*(exp(-1/(2*c^2))-1) - target
  }
}

# 碰撞函数反函数
g_i <- function(p) {
  uniroot(root_fun(p),lower = 1e-10, upper = 10, tol = 1e-5)$root
}


r1 <- 0.5
r2 <- 9.5

p1 <- 0.75
p2 <- 0.05 # 0.1 

w_lower <- r1 / g_i(p1) 
w_upper <- r2 / g_i(p2)

得到w_lower=1.595008,而w_upper=1.192211。此时上限小于下线，w不存在，说明概率设置过于苛刻。可以适当调高$p_2$的概率，设置为0.1，此时w_upper=2.393884，此时w的范围是合适的，接下来可以通过在此范围内选取一个合适的w。推荐的w选取策略：

  • 如果没有倾向性，选取区间的中间应该是一个不错的选择。
  • 如果需要准确率高，w取下限
  • 如果需要召回率高，w取上限。

选取L

为了方便最后的数据归并，强化的策略使用逻辑和嵌套逻辑与。设定逻辑和参数k=10，下面演示设计逻辑与数量L。

k <- 10 # 8

rho1 <- 0.99
rho2 <- 0.01

log(1-rho1) / log(1-p1^k) 
log(1-rho2) / log(1-p2^k)

L <- ceiling(log(1-rho1) / log(1-p1^k)) # 选取L
L

1-(1-p1^k)^L # 加强后的p1
1-(1-p2^k)^L # 加强后的p2

设定加强的目标的是$p_1=0.99,p_2=0.01$，加强之前分别是$p_1=0.75,p_2=0.05$。经过上面的计算，确定L=80可以达到加强效果。如果觉得L=80,数量过高，可以将k适当调整，比如k=8,得到的L=44。不过k过小，可能导致检索时，hash冲突过大，影响效率，所以这个地方需要权衡。

一站式参数评估(2019-2-23更新)

有些同学反馈上面两个R脚本使用较为困难，所以笔者给出下面更加简洁的参数评估R脚本，用户只需要输入r1(较近距离)和r2(较远距离)，即可评估出最佳hash单位长度$w$和桶的数量$L$。

##########################################################
# 一站式LSH参数评估
##########################################################

# 任意欧式距离在r1以内的两个点，碰撞的概率大于等于p1
r1 <- 0.5  # 根据数据特征分布适当修改
p1 <- 0.99 # 如果不知道算法细节，不要修改

# 任意欧式距离在r2以外的两个点，碰撞的概率小于等于p1
r2 <- 9.5 # 根据数据特征分布适当修改
p2 <- 0.01 # 如果不知道算法细节，不要修改

k <- 8 # 对应spark实现的桶宽度参数bucketWidth,推荐8~10

# 单轮LSH概率,如果不知算法道细节，不要修改下面两个参数
p1_one <- 0.75
p2_one <-  0.1 

# 碰撞函数
root_fun <- function(target) {
  function(c) {
    1-2*pnorm(-1/c) + (2*c/sqrt(2*pi))*(exp(-1/(2*c^2))-1) - target
  }
}

# 碰撞函数反函数
g_i <- function(p) {
  uniroot(root_fun(p),lower = 1e-10, upper = 10, tol = 1e-5)$root
}


w_lower <- r1 / g_i(p1_one) 
w_upper <- r2 / g_i(p2_one)
if (w_lower > w_upper) {
  stop("r2设置过低，或者r1设置过大，无法找到合适的w，请重新调整r1或r2！")
} else {
  print(sprintf("推荐w的范围[%.5f,%.5f],即spark实现的参数lshWidth",w_lower, w_upper))
  print(sprintf("如果要求准确率最高，推荐w=%.5f",w_lower))
  print(sprintf("如果要求召回率最高，推荐w=%.5f",w_upper))

  L_lower <- log(1-p1) / log(1-p1_one^k) 
  L_upper <- log(1-p2) / log(1-p2_one^k)
  L <- ceiling(L_lower) # 选取L
  if (L > L_upper) {
    stop("p1设置过低，或p2设置过大，无法找到合适的L，请重新调整p1或p2！")
  } else {
    print(sprintf("最优L=%d，即spark实现的参数bucketSize",L))
  }

  print(sprintf("加强后的p1=%.5f", 1-(1-p1_one^k)^L))
  print(sprintf("加强后的p2=%.5f",1-(1-p2_one^k)^L))
}

上面脚本会输出下面内容，

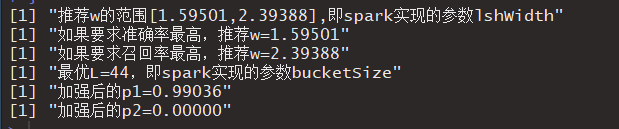
希望上面的内容对读者有帮助。

参考文献