PCA与聚类
最近一直在思考PCA是否可以辅助聚类(如kmeans),之前一直认为,如果数据集中如果有太多线性相关的数据,导致特征权重不平衡,会倾向线性相关的那些特征,导致掩盖其他特征。所以,如果通过PCA,是否找到背后关键的特征,避免这类问题。带者这个问题,开始了一次实验。
手动在3维空间中准备了4个类,数据生成代码如下,
set.seed(1234)
group_size <- 100
group1 <- data.frame(x1 = rnorm(group_size, mean=1),
x2 = rnorm(group_size, mean=1),
x3 = rnorm(group_size, mean=1),
group = 'red')
group2 <- data.frame(x1 = rnorm(group_size, mean=7),
x2 = rnorm(group_size, mean=7),
x3 = rnorm(group_size, mean=4.5),
group = 'green')
group3 <- data.frame(x1 = rnorm(group_size, mean=4),
x2 = rnorm(group_size, mean=3),
x3 = rnorm(group_size, mean=4.5),
group = 'blue')
group4 <- data.frame(x1 = rnorm(group_size, mean=5),
x2 = rnorm(group_size, mean=7),
x3 = rnorm(group_size, mean=10),
group = 'black')
data <- rbind(group1, group2, group3, group4)通过2d,3d或者MSD等可视化方法,可以清楚的观察到四个簇(下面是MSD绘图),
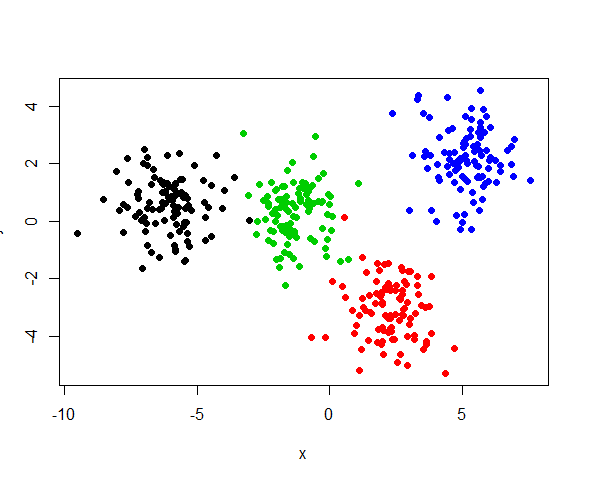
# 2d
pairs(data[,1:3],col=data$group)
# 3d
require(rgl)
require(car)
with(data,
plot3d(x1,x2,x3,col=group))
# MSD
dd <- dist(data[,1:3])
fit <- cmdscale(dd,eig=TRUE, k=2)
x <- fit$points[,1]
y <- fit$points[,2]
plot(x, y, pch=19, col = data$group)所以,根据之前的设想,如果添加很多线性相关的列,是否会有更多的簇呢(多余4个)?
derive_data <- cbind(data,
x4 = jitter(data$x1 + data$x2),
x5 = jitter(data$x2 + data$x3),
x6 = jitter(data$x1 + data$x3),
x7 = jitter(data$x1 + data$x2 + data$x3),
x8 = jitter(data$x1 + 2*data$x2 + 1.5*data$x3),
x9 = jitter(data$x1 + data$x2),
x10 = jitter(data$x2 + data$x3),
x11 = jitter(data$x1 + data$x3),
x12 = jitter(data$x1 + data$x2 + data$x3),
x13 = jitter(data$x1 + 2*data$x2 + 1.5*data$x3))
cor_dist <- dist(derive_data[,-4])
fit <- cmdscale(cor_dist,eig=TRUE, k=2)
x <- fit$points[,1]
y <- fit$points[,2]
plot(x, y, pch=19, col = derive_data$group)结果显示,即使添加了9个冗余的数据,MSD仍然可以清楚显示4个簇,
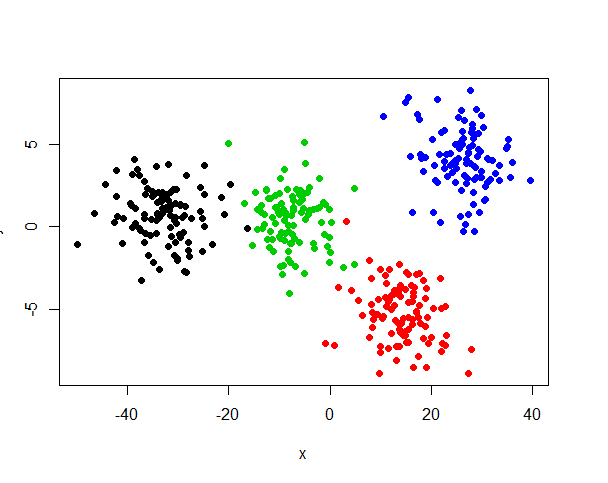
所以,根据这个实验,可以否定假设“线性相关会添加多余簇”。
下面试试PCA是否可以得到相关结果,
pca_mode <- princomp(derive_data[,-4])
plot(pca_mode)
summary(pca_mode)
pca_data <- predict(pca_mode,derive_data[,-4])
head(pca_data)
plot(pca_data[,1],pca_data[,2],col=derive_data$group, pch=19)根据PCA结果,只需要前2个组件就是解释99%+,
> summary(pca_mode)
Importance of components:
Comp.1 Comp.2 Comp.3 Comp.4 Comp.5
Standard deviation 23.0256553 3.75789335 2.113610716 1.236550e-03 1.216225e-03
Proportion of Variance 0.9661258 0.02573348 0.008140662 2.786332e-09 2.695490e-09
Cumulative Proportion 0.9661258 0.99185932 0.999999982 1.000000e+00 1.000000e+00
Comp.6 Comp.7 Comp.8 Comp.9
Standard deviation 1.188481e-03 1.164855e-03 1.110159e-03 1.058104e-03
Proportion of Variance 2.573915e-09 2.472598e-09 2.245845e-09 2.040172e-09
Cumulative Proportion 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00
Comp.10 Comp.11 Comp.12 Comp.13
Standard deviation 1.039415e-03 6.414794e-04 5.933439e-04 2.120504e-04
Proportion of Variance 1.968737e-09 7.498514e-10 6.415385e-10 8.193849e-11
Cumulative Proportion 1.000000e+00 1.000000e+00 1.000000e+00 1.000000e+00绘制2维散点图,仍然可以解释4个簇,
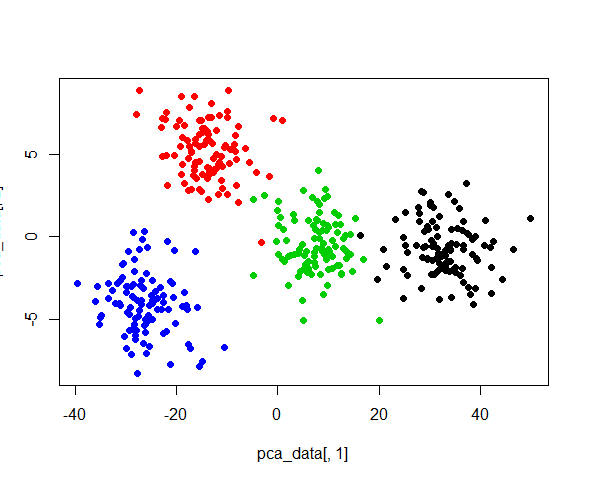
结论
根据这次结果,可以发现PCA与聚类结果没有直接的关系。可能的原因:PCA只是降低维度,簇并不一定与维度绑定,因为即使是1维空间,也可以明确的区分4个簇。PCA的作用顶多就是去掉噪音,减少计算量,并不会剔除簇信息,Cross Validated问答站点上有个类似回答,可参考How PCA would help the K-mean clustering analysis?。同时,根据上面的结果,线性相关变量也不一定会生成多余的簇。
试验代码
# 随机生成聚类数据
set.seed(1234)
group_size <- 100
group1 <- data.frame(x1 = rnorm(group_size, mean=1),
x2 = rnorm(group_size, mean=1),
x3 = rnorm(group_size, mean=1),
group = 'red')
group2 <- data.frame(x1 = rnorm(group_size, mean=7),
x2 = rnorm(group_size, mean=7),
x3 = rnorm(group_size, mean=4.5),
group = 'green')
group3 <- data.frame(x1 = rnorm(group_size, mean=4),
x2 = rnorm(group_size, mean=3),
x3 = rnorm(group_size, mean=4.5),
group = 'blue')
group4 <- data.frame(x1 = rnorm(group_size, mean=5),
x2 = rnorm(group_size, mean=7),
x3 = rnorm(group_size, mean=10),
group = 'black')
data <- rbind(group1, group2, group3, group4)
# 2d
pairs(data[,1:3],col=data$group)
# 3d
require(rgl)
require(car)
with(data,
plot3d(x1,x2,x3,col=group))
# MSD
dd <- dist(data[,1:3])
fit <- cmdscale(dd,eig=TRUE, k=2)
x <- fit$points[,1]
y <- fit$points[,2]
plot(x, y, pch=19, col = data$group)
# 添加线性组合
derive_data <- cbind(data,
x4 = jitter(data$x1 + data$x2),
x5 = jitter(data$x2 + data$x3),
x6 = jitter(data$x1 + data$x3),
x7 = jitter(data$x1 + data$x2 + data$x3),
x8 = jitter(data$x1 + 2*data$x2 + 1.5*data$x3),
x9 = jitter(data$x1 + data$x2),
x10 = jitter(data$x2 + data$x3),
x11 = jitter(data$x1 + data$x3),
x12 = jitter(data$x1 + data$x2 + data$x3),
x13 = jitter(data$x1 + 2*data$x2 + 1.5*data$x3))
cor_dist <- dist(derive_data[,-4])
fit <- cmdscale(cor_dist,eig=TRUE, k=2)
x <- fit$points[,1]
y <- fit$points[,2]
plot(x, y, pch=19, col = derive_data$group)
## pca
pca_mode <- princomp(derive_data[,-4])
plot(pca_mode)
summary(pca_mode)
pca_data <- predict(pca_mode,derive_data[,-4])
head(pca_data)
plot(pca_data[,1],pca_data[,2],col=derive_data$group, pch=19)您的打赏是对我最大的鼓励!
 支付宝打赏
支付宝打赏
 微信打赏
微信打赏