Macheine Learning for Trading 课程地址

这门课程主要介绍机器学习在股票交易中的应用，是佐治亚立功大学教授Tucker Balch开设的，他好像还参与创建了一个对冲基金公司，利用这门课程里的技术，进行基金运作。

本课程分为三个部分，前两个部分主要是介绍数据清理和领域知识，我直接跳过了，直接看第三部分。

Section 3.1 How Machine Learning is used at a hedge fund

第三部分，开始介绍什么是回归学习和一些常用模型。有一个demo令人映像深刻，使用KNN算法帮助机器人躲避障碍。其实本质上是一个二元分类问题，判断当前图片是否是障碍，如果不是就直接走，否则就换个方向。demo视频中的效果还不错。股票价格预测中，使用时间窗口切分训练和预测，与付费预测很类似。

Section 3.2 Regression

加农炮问题，使用参数方法（线性回归）求解，因为此问题可以用明确的数学方程来求解，所以可以通过数据学习参数。此问题是biased,因为我们会猜测这个方程的形式，二次，三角，指数等。

蜜蜂问题，由于问题无法用明确的数学公式求解，使用非参数（kNN）方法更为合适。无偏估计，因为使用均值。

Section 3.3 Assessing a learning algorithm

讲解overfitting，与之前的不太一样。之前横轴是样本量，而本教程用的模型参数，比如kNN，用k；决策树，树的深度；线性回归，多项式最大维度等。拐点就是最好的地方。

提到Roll forawrd Cross Validation. 这就是在预测数据评估时，不要使用时间较后的数据训练，预测较前的数据，这样可能新的数据带有之前数据的信息，有作弊嫌疑。传统的K-fold Cross Validation 就不太适用，好在我们历史数据很多，可以有很多组这种实验。点击预估，付费预估等问题，都是这样，使用较前的数据，预测较厚的数据，得到的评估效果才最贴近实际。

Secion 3.4 Ensemble learners, bagging and boosting

Ensemble

将不同模型合并起来，取均值。比如knn，lr，每一种算法可以通过调整参数，设置不同的复杂度，反正就是算出很多不同的模型。

Bagging

全称是Boostrap Aggregating,就是又放回的从训练集中取样，然后做成训练集合，最后训练m组，用同样的算法。得到不同的模型。随机森林就是用的这种思想。

有个比较好的例子，两个模型

  1. 1nn用于所有数据
  2. 10个1nn的模型，每个模型取60%数据。

2要好，多个模型最后合并去均值后，可以得到一个平滑的曲线。

Boosting

全称Adaptive Boost或Ada Boost。迭代计算。每轮迭代，将上一轮模型计算错误的例子，加大权重，随机选取。每个模型预测的权重，根据模型效果进行加权。GBDT使用此方法。

上面提到的三个算法称为meta algorithm,用于组装现有算法，如果LR，DT，SVM，kNN等。

Secion 3.5 Reinforcement Learning

增强学习的这套机制与购买股票的场景非常一致。

当前市场输入，指定策略，购买股票改变当前市场，得到反馈和收益，如此循环。

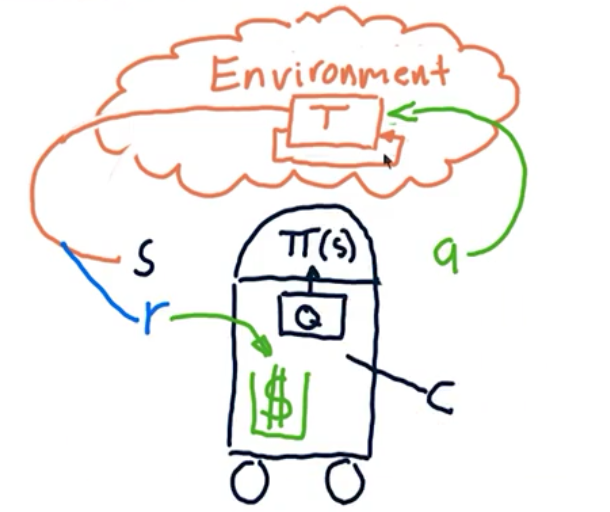
Markov Decision Problems

  • 状态集合S
  • 行为集合A
  • 转换函数T[$s,a,s^\prime$]，大多时候得不到
  • 回报函数R[s,a]，大多时候无法直接获得

如果上面的定义都清楚了，可以找到最优策略 $\pi^\star (s)$。常用算法

  • Policy Iteration
  • Value Iteration

通常转换矩阵和奖励函数不可得到，所以需要通过实验，构造四元组 $<s,a,s^\prime,r>$，然后拆分得到转换矩阵和奖励函数。最后使用算法Policy/Value Iteration得到最优策略，这种叫做Model-Based。 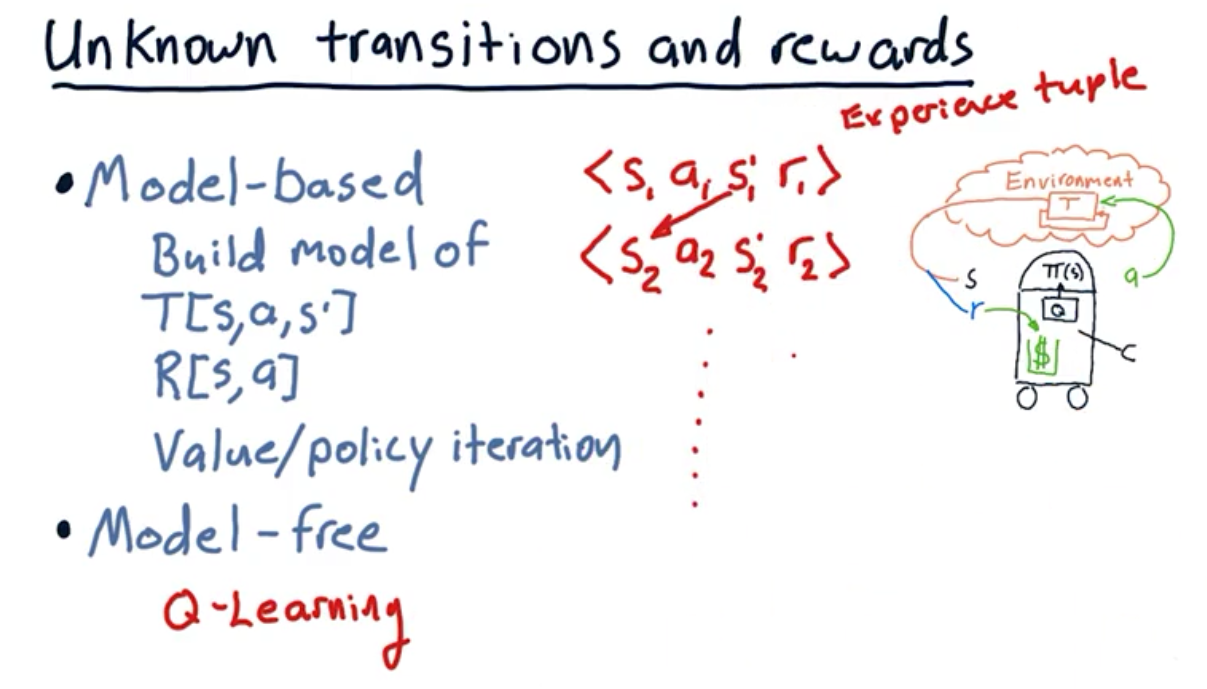Model-Free 使用Q-Learning算法，直接看四元组数据，构建策略，不用构建转换矩阵和奖励函数。

Section 3.6 Q-Learning

Q-Learing名称来源于Q函数

\[Q[s,a] = immediate\_reward + discounted\_reward\]

第二项是放眼未来，所以Q-Learning不是greedy的。问题求解，需要找到一个最优的a，

\[\pi (s) = \arg {\max_a{(Q[s,a])}}\]

最后得到的结果，$\pi^{\star}(s)$ 和 $Q^{\star}[s,a]$

更新规则，有点复杂没看懂，后面有机会再仔细研究

\[Q^{\prime}[s,a] = (1-\alpha)Q[s,a] + \alpha(r + \lambda Q[s^{\prime,},\arg {\max_a{(Q[s^{\prime},a^{\prime}])}}])\]

Section 3.7 Dyna-Q

加速Q-Learning收敛。