线代随笔10-马尔科夫矩阵的性质与估计

马尔科夫链可用于观察物体状态随时间的迁移模式，日常生活与工作中有大量的数据与状态有关。本文首先介绍马尔科夫矩阵的性质，然后介绍如何使用样本数据计算马尔科夫矩阵的数学推导，并且给出scala/spark实现的示例代码。

马尔科夫矩阵用于描述状态空间中，状态随机转移的过程。下一个状态只与当前状态有关，与其他状态无关。如下示例，

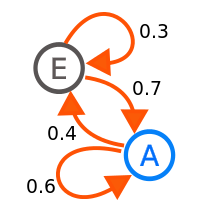
马尔科夫矩阵性质

马尔科夫矩阵定义

• $a_{ij} \ge 0$
• $\sum_{j=1}^{n}{a_{*j}} = 1$，（也可以是行，关键看A左乘还是右乘）

例1 \(A = \begin{bmatrix} 0.4 & 0.7 \\ 0.6 & 0.3 \\ \end{bmatrix}\)

性质1 $\lambda = 1$是特征值（可以先用上面的A试试）

证明：

设向量$1_n=\begin{bmatrix} 1 & \cdots & 1 \end{bmatrix}^T$

根据定义，上面必然成立！所以1是$A^T$特征值，根据特征值定义$A$与$A^T$特征值相同，所以1必然是$A$特征值。

证毕！

性质2 特征值$\lvert\lambda\rvert \le 1$

证明：

证明之前，先证明马科夫矩阵一个性质：如果$A$是马科夫矩阵，那么$A^n$仍然是马尔科夫矩阵。设一个函数——向量求和：$s(x) = \sum_{i=1}^nx_i$。在$A^2$的过程中，对于任意$[A^2]_l$列向量，计算向量和，

$[A^2]_{ij} \ge 0$，因为每个元素都是由大于0的元素相乘并相加得到，不可能得到负数。所以$A^2$是马尔科夫矩阵。同理，$A^3=A^2A$也是马尔科夫矩阵，最后可以归纳到任意$A^n$也是马尔科夫矩阵矩阵。

根据特征值的幂和特征向量$x$,可得$u=A^nx=\lambda^nx$，假设存在$\lvert \lambda \rvert > 1$，那么$u \rightarrow \infty $。但是$A^n$是马尔科夫矩阵矩阵，所以$A_{ij}\le 1$，所以$A^nx$不可能无限大，与已知矛盾，所以假设不成立。

证毕！

性质3 $A^nu_0$收敛

假设马科夫矩阵$A$有n个特征向量，且只有一个特征值为1的特征值$v_1$（绝大数实际情况的马尔科夫矩阵这这样）,根据之前课程中的内容，将其展开，

因为其他特征值据对值小于1，所以最后就收敛为$c_1x_1$。

例2 人口迁移例子，两个城市人口迁移

A <- matrix(c(.9,.2,.1,.8),byrow=T,nrow=2)
u0 <- matrix(c(0,1000))

A_eig <- eigen(A)
print(A_eig)

solve(A_eig$vectors, u0)[1,1]*A_eig$vectors[,1] # 理论结果

# 迭代验证
n <- 50
u <- u0
for(i in 1:n) {
  u <- A %*% u
  if(i <= 3 || i >=n-3){
    print(sprintf("i=%d",i))
    print(u)
  }
}

执行上面的代码，可以发现试验结果与理论结果一致。

马尔科夫矩阵估计

马尔科夫矩阵有这么好的形式，如何在实际问题中得到该矩阵呢？接下来介绍此过程，主要思路是使用马尔科夫转换的假设，构建目标函数，然后使用解答释然，求解极值，估计矩阵参数。由于该释然函数带有约束，使用拉格朗日乘子式将其变成无约束极值问题，最后得到估计值。

单对象目标函数

首先，定义一些符号，

• $X^n$表示随机序列，长度为n。$x^n \equiv x_1,x_2,\cdots, x_n$表示该随机序列样本。
• $X_n$表示随机状态，$x_n$表示样本。（注意：n在X右上与右下的意义是不同的。）
• $p_{ij}=Pr(X_n=j\|X_{n-1}=i)$表示状态从i到j的概率。
• $n_{ij}$表示状态从i到j的样本个数。
• k为状态的数量

那么出现样本$x^n\equiv x_1,x_2,\cdots, x_n$的概率如下

上面的等式中，第一，二行直接使用条件概率，计算样本概率，第三行利用了马尔科夫链的性质，即第t个状态只与t-1的状有关，与之前的状态无关。由于各个状态转换是固定的，变的是不同转换的次数，所以上面的等式可以换一种方式表示，如下：

多对象目标函数

现在概率公式已经化简的比较简单了，但是还有一个问题：现在只观察了一个对象的转换序列，如果多个对象呢？接下来，将上面的公式对m个对象进行扩展，先定义一些补充变量，

• 总共有$m$个对象。
• $X(l)^n$是第$l$个对象的随机序列。
• $X(l)_n$是第$l$个对象的第n个状态的随机变量。
• $n(l)$表示第$l$个对象的状态转换次数。
• $n(l)_{ij}$表示第$l$个对象状态从i到j的样本个数。
• $N_{ij} = \sum_{l=1}^m{n(l)_{ij}}$，表示所有样本中状态i到j的样本数。

并且，假设m个对象相互独立，目标函数设为$L(p)$，扩展后的样本概率为

带约束的优化

现在的工作就是找到L(p)最大时对应的转换矩阵p，L(P)的最大值并不关注。由于连乘不太方便计算，所以对$L(p)$取自然对数，由于$\ln$是单调递增，所以当$\ln{L(p)}$最大时，p与L(p)最大时的p一致。所以，现在转换成了一个优化问题，如下：

上面的目标函数比较简单，但是不要忘记，有约束条件：

带有约束的最优化是无法直接求导计算的，因为计算结果可能不遵守约束，所以，需要将约束去掉，转成等价的无约束优化问题，使用拉格朗日乘子数，变化结果如下：

相比于之前目标函数，$\mathcal{L}(p)$多了$k$个变量$\lambda_{i}, i \in (1,\cdots,k)$,现在分别对所有变量计算偏导，

对于$\lambda_{i}$的偏导，得到如下：

上面就是约束条件，意义是极值在这个条件下确实可以得到！

接着，对$p_{ij}$计算偏导，得到如下：

将(2)代入(1),可以得到：

将(3)代入(1)，得到$p_{ij}$

推导完毕！

应用实践

最后的结论非常简洁优雅：每类转换次数比上所有同源转换次数。此时，得到此样本的概率最大。

理论推导完毕，最后给出spark的实现，仅供参考：

import org.jblas.DoubleMatrix

val transitionData:RDD[Vector] = ... //
val n = ... // 状态个数

// 统计转换次数
val transitionMatrixCount = transitionData.map(transition => {
	val transitionMatrix = DoubleMatrix.zeros(n, n)
	for (i <- 0 until (transition.size - 1)) {
		val (current, next) = (transition(i).toInt, transition(i + 1).toInt)
		val currentCount = transitionMatrix.get(current, next)
		transitionMatrix.put(current, next, currentCount + 1)
	}
	transitionMatrix
}).reduce((left, right) => left.add(right))

// 统计每类次数
val rowSums = transitionMatrixCount.rowSums()

// 计算最后的转换矩阵
val transitionMatrixRate = DoubleMatrix.zeros(n, n)
for (i <- 0 until n) {
	for (j <- 0 until n) {
		val rate = transitionMatrixCount.get(i, j) / rowSums.get(i)
		transitionMatrixRate.put(i, j, rate)
	}
}

println(transitionMatrixRate.toString("%.4f","","",",","\n"))

实际运行效果：3亿条转换序列（4千万对象，平均每个对象8次转换），spark设置80个executors,每核分配10G内存，计算需要3分钟。

总结

本文推导了马尔科夫矩阵的评估方法，并且给出了spark的实现。但是，推导中有两条重要假设

• t状态转换只与t-1有关
• 用户之间独立

大多数实际情况下，上面两个条件是很难达到的，所以应用上面推导结论时，遇到不可解释的现象，可能是由于上面的假设被严重的破坏，这时可能就需要换用其他方法。比如，分析用户社交行为时，用户之间独立就不成立。在比如，有新的大版本上线，改变了整体用户行为，导致整个转换出现了变化。但是，总体来说，注意了上面的情况，一般没太大问题。

参考资料

• 马尔科夫链
• 拉格朗日乘子式
• Note: Maximum Likelihood Estimation for Markov Chains