正定矩阵是一种特殊的对称的矩阵，很多应用中都会涉及正定矩阵的相关性质。正定矩阵比较有趣的一点是，它可以将线性代数中很多重要的概念串联起来，形成一个整体。本文主要描述正定矩阵的性质以及各性质之间的关系，并且给出相关证明。

对称矩阵$A$具有下面5个性质中的一个，那么它就具备了剩下的其他性质，并且被称之为正定矩阵:

  1. 所有主元大于0
  2. 所有左上行列式大于0
  3. 所有特征值大于0
  4. $x^TAx \gt 0, x \ne 0$
  5. $A=R^TR$并且R的列线性独立

上面有5个性质，如果每两个互相证明，那么需要证明20个定理，非常繁琐。其实，可以用图的角度看待这个问题，将每个性质看作图的顶点，如果性质之间具有推导特性，看作一条有向边。只要任意一个点出发，都可以到达其他顶点，那么问题就解决了，并且需要证明的定理也不需要20个。经过观察，可以得到下面的推导图，

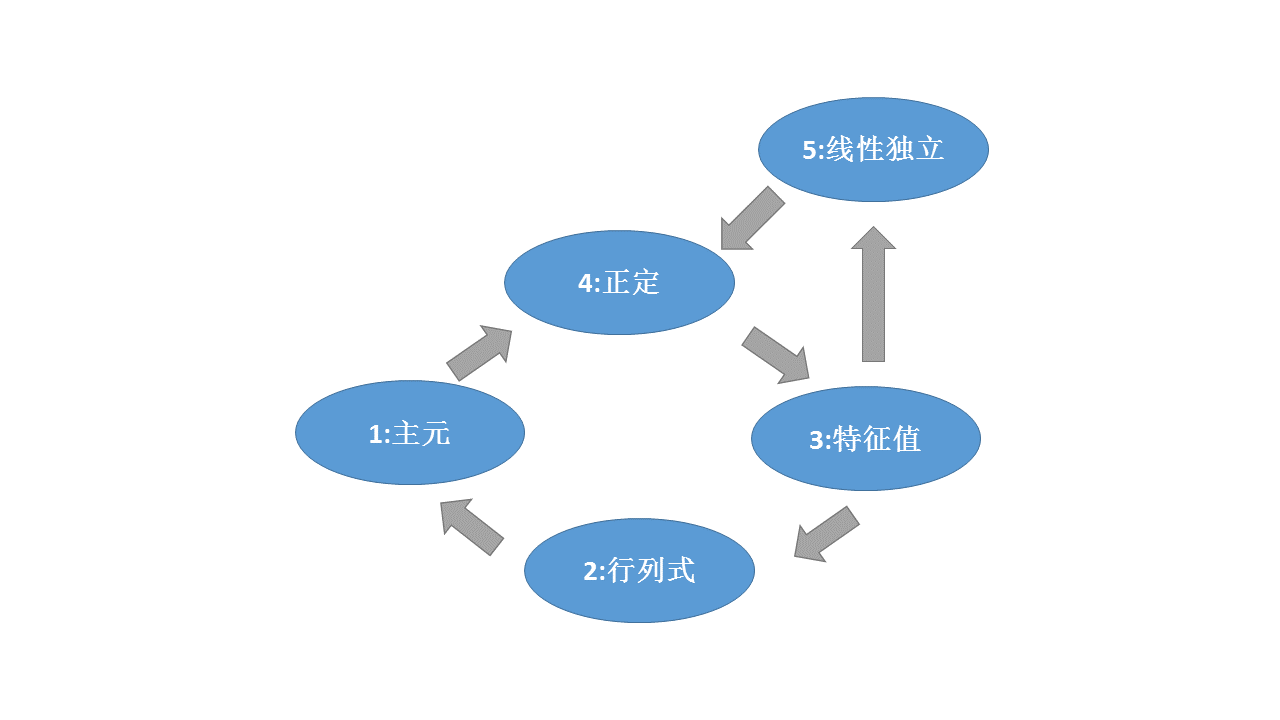
根据上面的推导图，现在只需要证明6个定理，即可达到目的，下面逐个证明。

证明：4 $\Rightarrow$ 3

命题 若对称矩阵A有性质$x^TAx \gt 0, x \ne 0$，证明A的所有特征值均为正数。

证明

A对称，那么其必然可以对角化，有$A=Q \Lambda Q^T$,且将正定性质代入，具有$x^TQ \Lambda Q^Tx \gt 0$，其中$\Lambda$是对角矩阵，对角元素为$\lambda_1, \cdots, \lambda_n$。令$y = Q^Tx=\begin{bmatrix}y_1 && \cdots && y_n\end{bmatrix}^T$。所以，最后有

\[y\Lambda y^T>0 \Rightarrow \sum_{i=1}^{n}\lambda_i y_i^2 > 0\]

上述不等式需要对任意不等于0向量的x成立，由于$Q^T$是标准正交矩阵，也就是对任意不等于0向量的y成立，所以$\lambda_i > 0$必须横成立。

证毕

证明：3 $\Rightarrow$ 5

命题 若对称矩阵A所有特征值大于0，证明存在矩阵R，其列线性独立，且$A=R^TR$。

证明

A对称，所以有$A=Q \Lambda Q^T$。因为条件$\lambda_i > 0$，所以有$A=Q \Lambda^{\frac{1}{2}} (\Lambda^{\frac{1}{2}})^T Q^T$，令$R=(Q \Lambda^{\frac{1}{2}})^T$,且$R^{-1}=Q\Lambda^{-\frac{1}{2}}$，那么有R可逆且$A=R^TR$。

证毕

证明: 5 $\Rightarrow$ 4

命题 对称矩阵A有$A=R^TR$并且R的列线性独立，证明 $x^TAx \gt 0, x \ne 0$

证明

因为R列线性独立，$x\ne 0$，所以$Rx \ne 0$。

直接按照条件展开$x^TAx=x^TR^TRx=(|Rx|)^2>0$恒成立。

证毕

证明：3 $\Rightarrow$ 2

命题 对称矩阵A的所有特征值大于0，证明A的所有左上行列式大于0

证明

因为A所有特征值$\lambda_i \gt 0$，所以有$|A| = \prod_{i=1}^{n}\lambda_i \gt 0$。

假设$A_k$是矩阵A保留左上角k行和k列。因为对任意$x \ne 0$，均有$x^TAx \gt 0$,所以对于特殊形式的$x=(x_1,x_2,\cdots,x_k,0,\cdots,0)\ne 0, k = 1,2,\cdots,n$仍然成立，则$A_k$与A有如下关系

\[\begin{align} 0 <& (x_1,x_2,\cdots,x_k,0,\cdots,0)A(x_1,x_2,\cdots,x_k,0,\cdots,0)^T \\ =& (x_1,x_2,\cdots,x_k) A_k (x_1,x_2,\cdots,x_k) \end{align}\]

所以$A_k$所有特征值大于0（利用$4 \Rightarrow 3$），所以$|A_k| \gt 0$。

证毕

证明：2 $\Rightarrow$ 1

命题 对称矩阵A所有左上行列式大于0,证明A的所有主元大于0

证明

因为$|A_k|>0$，所以A可逆。那么，可以只通过基础消元（特征值不变），而不需要基础换行或基础乘法（这些导致特征值变化），将A化简为只有$主对角线$的矩阵，此时对角线上的元素就是主元$p_i$，并且此过程做上角行列式保持不变。所以有$|A_k|=\prod_{i=1}^kp_i,|A_{k-1}|=\prod_{i=1}^{k-1}p_i$,推导出$p_k=\frac{|A_k|}{|A_{k-1}|}>0$。

证毕

证明：1 $\Rightarrow$ 4

命题 对称矩阵A所有主元大于0，证明$x^TAx > 0,x \ne 0$

证明

使用LDU分解，由于A对称，所以$A=LDL^T$，其中D是对角矩阵，且每个元素$p_i$是A的主元。代入x，有$x^TLDL^Tx$。令$y=L^Tx=(y_1,y_2,\cdots,y_n)$。所以$x^TLDL^Tx=y^TDy=\sum_{i=1}^np_iy_i^2>0$。

证毕

至此，所以必要的定理已经证明完成，得到了完成的证明图，最终的问题得到了证实。