基于LSTM的序列自编码实践
背景
序列数据在工作中经常出现,比如
- 用户在某款APP的活跃频率序列
- MOBA游戏中使用英雄的序列
- 游戏日活跃用户数序列曲线
最近流行的深度学习,可以很方便的处理这类数据,要么直接用序列数据作为输入,处理分类或回归问题;要么将序列数据embedding成固定长度的向量,作为其他模型的输入。对于后者,笔者特别有兴趣,因为可以给现有的模型提供更丰富的特征,可以得到更好模型效果。本文将介绍基于LSTM的seq2seq序列自编码,使用TensorFlow的python接口实现,主要参考(2014)Sequence to Sequence Learning with Neural Networks。
TensorFlow的工作流程简介
TensorFlow最近在深度学习社区异常火爆,因为有Google为其站台。不过说实话,其原生API不是特别友好,有一定门槛,无法快速开发原型,相比于Keras的易用性,差远了。好在TensorFlow将keras包括在内,所以可以直接在TensorFlow中使用Keras。不过,由于序列自编码的特殊性,笔者还是使用TensorFlow的原生API构建了整个架构,因为使用keras很难处理一些细节。
TensorFlow一开始需要构建计算图,构建完后,才能通过Batch SGD一点一点的逼近最优解。构建计算图的过程,可以类比为Spark RDD中的transform操作,执行Batch SGD可以类比为action操作。在构建计算图时,数据没有真实执行,只有在构建计算图后,通过特殊的优化tensor,使得Loss逐步收敛。
网络架构与实现
序列自编码的架构如下
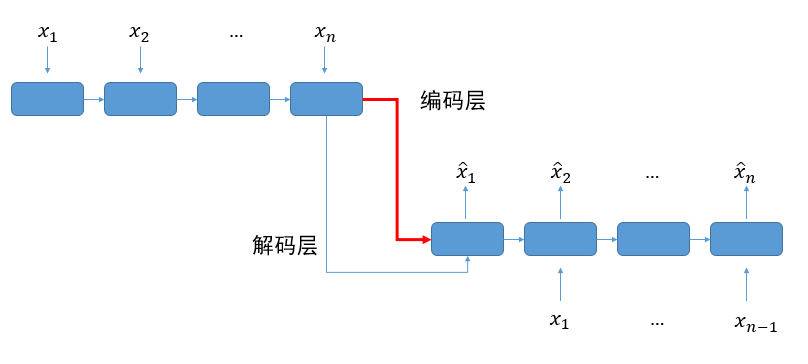
工作流程
上面一层是编码层,使用LSTM作为基础模块,中间红色箭头表示最后的编码向量。将编码层的最后一个输出,加上原始输入作为解码层的输入,但是需要去掉原始输入的最后一个输入。最后使用平方错误,评估自编码的效果。
代码解读
下面是比较枯燥的编码环节,如果只关心最终效果,可以跳过,直接阅读下节实验效果。 笔者将整个计算图的构建过程封装到类RNNAutoEncode中,其接口如下
class RNNAutoEncode(object):
"""
Reference paper https://arxiv.org/abs/1409.3215
"""
def __init__(self, series, series_length,
hidden_num, feature_num, max_series,
learning_rate=0.0001, layer_num=1,
activation=tf.nn.tanh):series和series_length是序列和对应真实长度,不足的长度需要padding。hidden_num是编码长度。feature_num是序列每个单元的特征数量。max_series表示最大序列长度。
# Encoding layer
encode_cell = tf.contrib.rnn.MultiRNNCell(
[tf.contrib.rnn.BasicLSTMCell(hidden_num, reuse=False, activation=activation)
for _ in range(layer_num)]
)
encode_output, self.encode_final_state = tf.nn.dynamic_rnn(
encode_cell, series, sequence_length=series_length, dtype=tf.float32, scope='encode')设置编码层,默认只有一层lstm编码层,激活函数使用tanh,与LSTM兼容性较好,若使用relu,基本上无法收敛。self.encdoe_final_state是最后的编码结果,所以作为成员变量,方便后面引用。dynamic_rnn中提供了sequence_length长度,方便tensorflow内部自动截取有效数据。
encode_weight = tf.Variable(tf.truncated_normal([hidden_num, feature_num]))
encode_bias = tf.Variable(tf.constant(0.1, shape=[feature_num]))
last_encode_output = tf.gather(encode_output, axis=1, indices=max_series-1)
last_encode_output = tf.expand_dims(last_encode_output, axis=1)
last_encode_output = tf.map_fn(lambda out: tf.matmul(out, encode_weight)+encode_bias, last_encode_output)
print("Last encode output shape", last_encode_output.get_shape())需要将编码层的最后一个输出作为解码层的第一个输入,但是由于hidden_num与feature_num可能不兼容,所以需要使用encode_weight和encode_bias转换last_encode_output。
# Decoding layer
input_without_last = tf.slice(series, begin=[0, 0, 0], size=[-1, max_series - 1, feature_num])
decode_input = tf.concat([last_encode_output, input_without_last], axis=1)
print("Decode input shape", decode_input.get_shape())将输入序列的最后一个单元剔除,然后在前面添加上last_encode_ouput,作为编码层的输入。如果只用0填充第一个单元,那么会导致loss不收敛。
decode_cell = tf.contrib.rnn.MultiRNNCell(
[tf.contrib.rnn.BasicLSTMCell(hidden_num, reuse=False, activation=activation)
for _ in range(layer_num)]
)
decode_cell_output, _ = tf.nn.dynamic_rnn(decode_cell, decode_input, initial_state=self.encode_final_state, dtype=tf.float32, scope='decode')
print("Decode cell output shape", decode_cell_output.get_shape())编码过程与解码过程基本类似,但是将self.encode_final_state作为initial_state,用于传递编码信息。
decode_weight = tf.Variable(tf.truncated_normal([hidden_num, feature_num]))
decode_bias = tf.Variable(tf.constant(0.1, shape=[feature_num]))
padding_weight = tf.map_fn(
lambda length: tf.concat(
[tf.ones(shape=(length, feature_num), dtype=tf.float32),
tf.zeros(shape=(max_series - length, feature_num), dtype=tf.float32)], axis=0),
series_length,
dtype=tf.float32)
print("Padding Weight", padding_weight)
decode_output = padding_weight*tf.map_fn(lambda unit: tf.matmul(unit, decode_weight)+decode_bias, decode_cell_output)
print("Decode output shape", decode_output.get_shape())解码的向量与原始输出也不兼容,所以需要用decode_weight与decode_bias转换。由于原始输入是经过padding,所以解码的输出也只需要考虑series_length范围内的解码内容,其他的用0替代,使用padding_weight转换相关数据。
# Loss Function
self.loss = tf.losses.mean_squared_error(labels=series, predictions=decode_output)
print("Loss", self.loss)
# Optimizer
optimizer = tf.train.GradientDescentOptimizer(learning_rate=learning_rate)
self.train = optimizer.minimize(self.loss)最后,设置平方错误loss和优化器Batch SGD,整个计算图的构建完毕。整体调用方法,参考test_auto_encode_demo.py。
实验效果
实验数据
人工设置了是三个序列:$sin(0.5x)$,$sin(2x)$和$tanh(x)$。数据区间为$[-\frac{3}{2}\pi,\frac{3}{2}\pi]$。sin函数为周期函数,可以观察自编码是否可以提取周期信息。$tanh(x)与sin(0.5x)$在此区间比较相似,可以观察自编码是否可以找到相似序列的区别。当然,任务不能这么简单,在原始曲线上添加了一些噪音,使得任务更加困难,具体的数据生成代码,可以参考这里,下面是原始数据和添加噪音后的数据。添加噪音后,肉眼比较难以区分$sin(0.5x)$与$tanh(x)$。
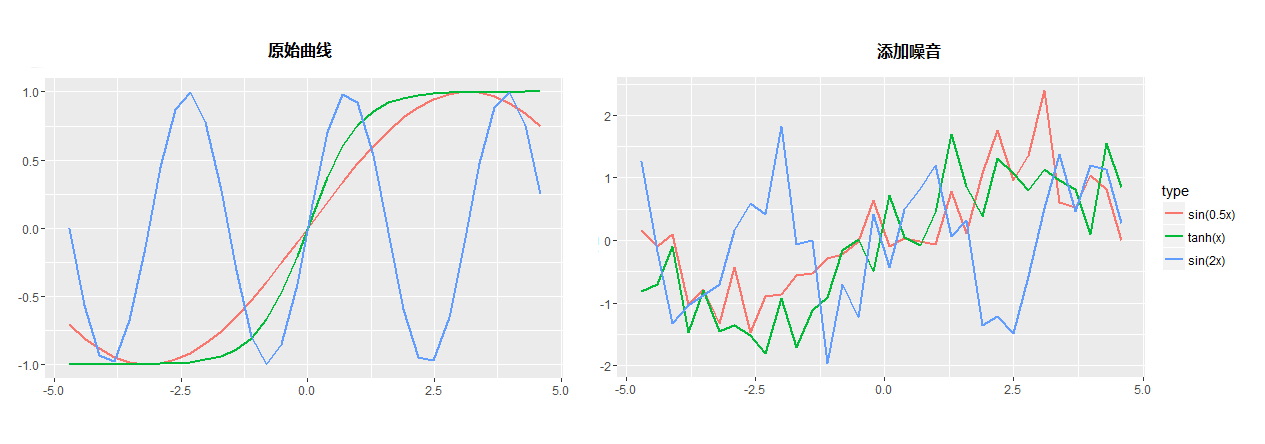
实验过程
数据生成后,使用上面实现的RNNAutoEncode将其编码。通过TensorBoard,可以看到loss还是得到了有效的收敛,灰色为训练loss,橙色为测试loss。
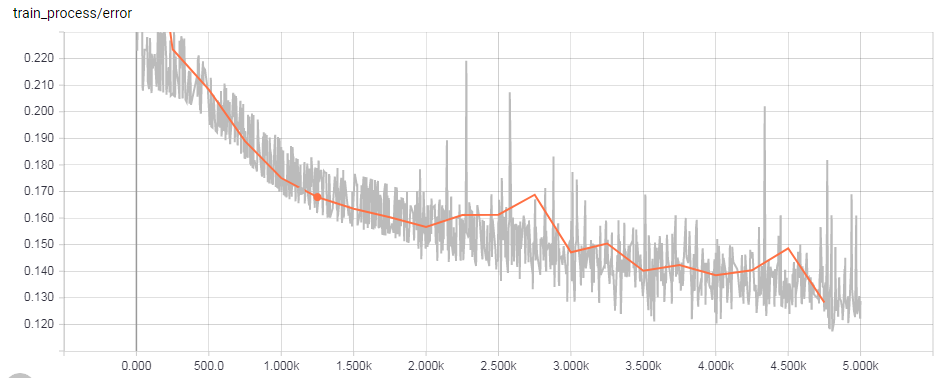
将得到的编码数据,使用PCA可视化,观察三类曲线是否有显著的区分。
实验结果
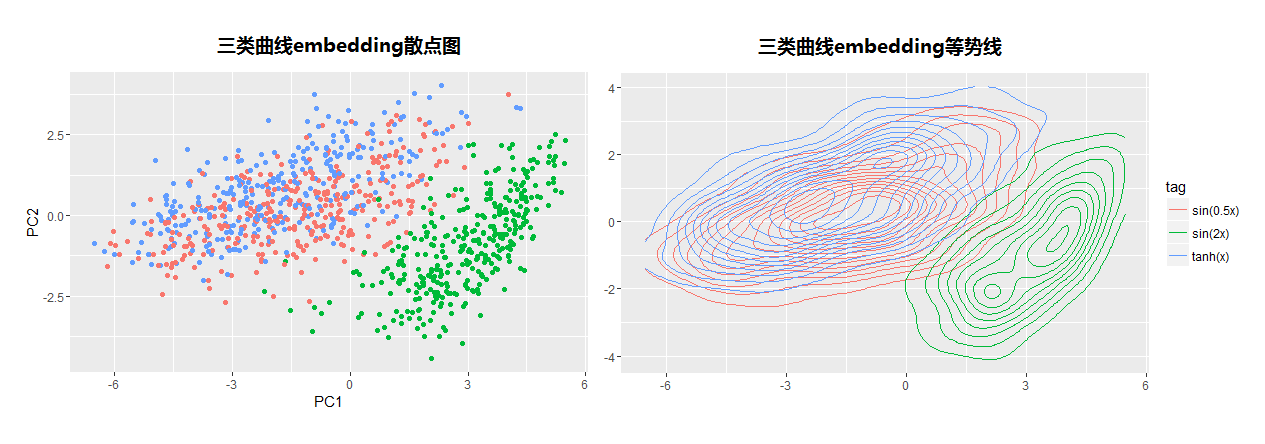
根据上面的数据,可以发现周期函数$sin(2x)$还是被有效与其他两个序列区分开。但是由于序列$sin(0.5x)$与$tanh(x)$非常类似,尤其是在加上噪音后,所以区分能力不是很明显,但是如过逐步减少噪音方差,autoencode还是可以很明显的将$tanh(x)$与$sin(0.5x)$分开,有兴趣的读者可以clone项目,尝试减少方差,看看效果。
写在最后
经过这次试验,基本掌握了TensorFlow的开发模式,后续可以应用于工作中。基于LSTM的自编码
- 可以有效编码不同周期的序列
- 对于曲线类似的序列,有一定的区分能力,区分能力与噪音程度相关
笔者还尝试了使用标签进行序列自编码,实际用途不是特别大,因为标签一般很难得到,效果也很一般。
现在处理序列数据,多了一项常规武器—自编码RNNAutoEncode。当然,需要改进的地方应该还有很多,需要在实践中不断打磨,验证其效果。
最后感谢bolansu,xiaoxiwang和yasarwang的帮助,给了笔者很多启发。
您的打赏是对我最大的鼓励!
 支付宝打赏
支付宝打赏
 微信打赏
微信打赏