强化学习笔记07-策略梯度

Value-Based与Policy-Based

RL问题，本质上是求解一个policy函数，policy类似监督学习中的model。之前求解policy都是通过间接的方式，即根据最大Q(s,a)获取执行动作。Policy Gradient不同，直接将policy放到求解问题中，通过梯度方法直接获取最优policy函数。Policy Gradient的解法属于RL问题解法中的另外一个流派，policy-based；之前提到的解法，属于value-based。这些解法的关系参考下面，

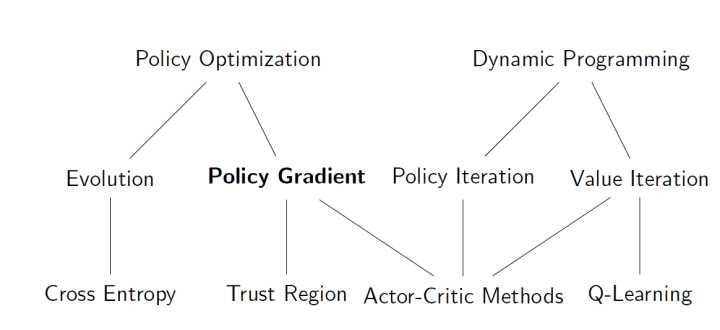
Policy Gradient的优缺点总结如下

优点
- 收敛性质好
- 可以应用于高纬度连续动作空间
- 可以学习随机策略
缺点
- 一般情况收敛到局部最优
- 策略评估效率低且方差大

举个例子，理解如何学习到随机策略。

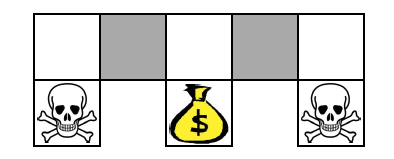
上面一个地图，agent可以移动，遇到骷髅结束，遇到金币获得奖励，其他获得负的奖励。在灰色地带，agent无法区分两个灰色地带，即agent无法知道是在左边的灰色还是右边的灰色。

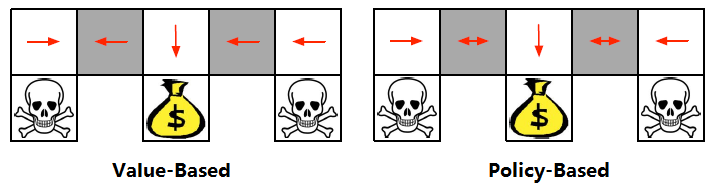
上面左图是Value-Based的学习的策略，如果agent不幸走到左边，会在那里来回震荡。而右图是Policy-Based的策略，在灰色地带，动作在两边都有概率，无论agent在哪里，都不会出现来回震荡。

何为称作Policy Gradient？

为了求解最优函数 $\pi_\theta(s,a)$ ，需要构建一个目标函数，然后用各种最优化方法求解，得到最优函数。

阶段(Episodic)场景，使用开始状态的值函数作为目标函数， $J_1(\theta)=V^{\pi_\theta}(S_1)=E_{\pi_\theta}[V_1]$
连续(Continuous)场景，使用平均值函数， $J_{avV}(\theta)=\sum_s d^{\pi_\theta}(s)V^{\pi_\theta}(s)=\sum_s d^{\pi_\theta}(s)\sum_a \pi_\theta(s,a) R_s^a$

所以，将此问题转成一个最优化问题（套路与监督学习非常类似），优化问题的解法非常多，这里专注梯度解法。并且，此最优化问题是求最大值，所以参数更新方法是梯度递增（Gradient Ascent）而不是梯度递减。即 $\Delta \theta = \alpha \nabla_\theta J(\theta)$ 。这也就是Policy Gradient的由来，通过Gradient求解Policy。

梯度有时候不能太好计算，尤其是那些复杂的目标函数，但是可以通过有限差分初步估算梯度，原理是在梯度点附近，通过泰勒展开，保留线性部分，剔除其他余项，类似计算切线斜率，方法如下

\frac{\partial J (θ)}{\partial θ_{k}} \approx \frac{J (θ + ϵ u_{k}) - J (θ)}{ϵ}

$\frac{\partial J(\theta)}{\partial \theta_k} \approx \frac{J(\theta+\epsilon u_k) - J(\theta)}{\epsilon}$

可以看到，只需要定义步长 $\epsilon$ ，无需求解梯度，十分方便。

得分函数Score Function

得分函数是Policy Gradient求解过程中的一个通用形式，对 $\nabla \pi_\theta(s,a)$ 变形，

\nabla π_{θ} = π_{θ} (s, a) \frac{\nabla π_{θ} (s, a)}{π_{θ} (s a)} = π_{θ} (s, a) \nabla \ln (π_{θ} (s, a))

$\nabla \pi_\theta = \pi_\theta(s,a) \frac{\nabla \pi_\theta(s,a)}{\pi_\theta(sa)} = \pi_\theta(s,a) \nabla \ln{\left(\pi_\theta(s,a)\right)}$

其中， $\nabla_\theta \ln{\pi_\theta(s,a)}$ 称为得分函数，后面会经常遇到。此函数有一个比较好的性质，对数函数会将乘法变成加法，这样非常方便求导。

比如使用Softmax和线性模型构建策略函数，

π_{θ} (s, a) = \frac{e^{ϕ (s, a)^{T} θ}}{\sum_{b} e^{ϕ (s, b)^{T} θ}}

$\pi_\theta(s,a) = \frac{e^{\phi(s,a)^T \theta}}{\sum_b e^{\phi(s,b)^T \theta}}$

对应得分函数形式如下，

\nabla \ln π_{θ} (s, a) = ϕ (s, a)^{T} - \sum_{b} π_{θ} (s, b) ϕ (s, b) = ϕ (s, a)^{T} - E_{π_{θ}} [ϕ (s, *)]

$\nabla \ln{\pi_\theta(s,a)} = \phi(s,a)^T - \sum_b \pi_\theta(s,b) \phi(s,b) = \phi(s,a)^T - E_{\pi_\theta}[\phi(s, *)]$

上式计算技巧：不要用ln与分母过早的结合，而是先求导，然后得到策略函数。

在比如，在连续动作场景，一般假设动作a符合正太分布，其分布均值与状态s有关，方差认为设定为 $\sigma$ ，那么 $a \sim N(\mu(s), \sigma^2)$ 。此时， $\pi_\theta(s,a)$ 是正太分布的概率密度，代入得分函数得后形式非常简单

\nabla \ln π_{θ} (s, a) = \frac{(a - μ (s)) ϕ (s)}{σ^{2}}

$\nabla \ln {\pi_\theta(s,a)} = \frac{(a - \mu(s))\phi(s)}{\sigma^2}$

一步MDP

在一步的情况下，epsoide和continues的场景是一致的，可以用即时奖励作为回报，即 $r=R_s^a$ ，代入到目标函数中

J (θ) = E_{π_{θ}} [r] = \sum_{s \in S} d (s) \sum_{a \in A} π_{θ} (s, a) R_{s, a}

$J(\theta) = E_{\pi_\theta}[r] = \sum_{s \in S}d(s)\sum_{a \in A} \pi_\theta(s,a) R_{s,a}$

对目标函数求导，代入得分函数，

\nabla_{θ} J (θ) = \sum_{s \in S} d (s) \sum_{a \in A} π_{θ} (s, a) ((\nabla_{θ} \ln π_{θ} (s, a)) R_{s, a}) = E_{π_{θ}} [(\nabla_{θ} \ln π_{θ} (s, a)) r]

$\nabla_\theta J(\theta) = \sum_{s \in S} d(s) \sum_{a \in A} \pi_\theta(s,a) ((\nabla_\theta \ln \pi_\theta(s,a)) R_{s,a}) = E_{\pi_\theta} [(\nabla_\theta \ln \pi_\theta(s,a)) r]$

Policy Gradient定理

该定理将一部MDP泛化到多步MDP，主要是用长期回报估计 $Q^\pi(s,a)$ 替换即时奖励 $R_s^a$ 。后面将要介绍的一些列估算算法也是在奖励这块变化，得到不同的衍生算法。

REINFORCE算法

PolicyGradient的Monte-Carlo版本，大致思路沿用前面提到的方法。只是将 $r$ 换成 $v_t$ 的无偏估计，伪代码如下

此算法具有MC类算法的统一缺点，效率低，收敛慢。同时，其方差还比较大。

Actor-Critic算法

RINFORCE算法方差很大，可以使用评论家(Critic)评估行为值函数，而不是MC采样，即 $Q_w(s,a) = Q^{\pi_\theta}(s,a)$ ，实验证明这样可以有效减少方差，提高训练效率。Actor更新策略参数 $\theta$ ，critic更新行为值函数的参数 $w$ 。critic做的事情就是行为值函数评估，之前的章节已经讨论过，可以使用MC，TD，TD( $\lambda$ )等方法完成。下面举个列子，使用线性模型模拟行为值函数，使用TD(0)评估行为值函数，此算法称为QAC，伪代码如下

此方法效率比MC高，无需等待评估 $v_t$ 可以逐步在线学习。

Bias和避免方法

Actor-Critic算法存在bias，因为Critic是biasd，所以根据biased的数据学习的策略也是biased。幸运的是，如果适当的选取Critic的近似函数，可以确保整个过程not biased。近似函数 $Q_w(s,a)$ 需要满足下面两点，

$\nabla Q_w(s,a) = \nabla_\theta \ln \pi_\theta (s,a)$ ，行为值函数的梯度向量与值函数的梯度向量相同。
$\varepsilon = E[(Q^{\pi_\theta}(s,a)-Q_w(s,a))^2]$ ， $w$ 用于最小化 $\varepsilon$ 。

此时， $\nabla_\theta J(\theta) = E_{\pi_\theta}[(\nabla_\theta \ln \pi_\theta(s,a)) Q_w(s,a)]$ 无偏移。证明过程比较简单，直接按定义展看即可。所以，得分函数在Actor-Critic过程中非常重要。

减少Variance

之前提到REINFORCE有较大Variance，但是使用一个基础函数B(s)，只要与动作action无关，对梯度没有影响，但是可以有效减少Variance。值函数V(s)与动作无关，一般可以作为比较好的基础函数。令 $A^{\pi_\theta}(s,a) = Q^{\pi_\theta}(s,a) - V^{\pi_\theta}(s)$ ,用A代替Action-Critic中的r，可以有效减少variance。

但是，这样需要而外计算值函数，所以现在需要计算三套参数，

$V_v(s) \approx V^{\pi_\theta}(s)$
$Q_w(s,a) \approx Q^{\pi_\theta}(s,a)$
$\pi_\theta(s,a) \approx \pi (s,a)$

这不是增加了计算负担了？其实不是，回忆TD方法评估值函数，每次更新方法为

δ^{π_{θ}} = r + γ V^{π_{θ}} (s^{'}) - V^{π_{θ}} (s)

$\delta^{\pi_\theta} = r + \gamma V^{\pi_\theta}(s^\prime) - V^{\pi_\theta}(s)$

此更新方法恰巧是优势函数 $A^{\pi_\theta}(s,a)$ 的无偏估计,

E_{π_{θ}} [δ^{π_{θ}} | s, a] = E_{π_{θ}} [r + γ V^{π_{θ}} (s^{'}) | s, a] - V^{π_{θ}} (s) = Q^{π_{θ}} (s, a) - V^{π_{θ}} (s) = A^{π_{θ}} (s, a)

$E_{\pi_\theta}[\delta^{\pi_\theta}|s,a] = E_{\pi_\theta}[r + \gamma V^{\pi_\theta}(s^\prime) \vert s,a] - V^{\pi_\theta}(s) = Q^{\pi_\theta}(s,a) - V^{\pi_\theta}(s) = A^{\pi_\theta}(s,a)$

所以，可以使用TD错误计算梯度，并且只需要两组参数，而不是三组，最后梯度为

\nabla_{θ} J (θ) = E_{π_{θ}} [(\nabla_{θ} \ln π_{θ} (s, a)) (r + γ V_{v} (s^{'}) - V_{v} (s))]

$\nabla_\theta J(\theta) = E_{\pi_\theta}[(\nabla_\theta \ln \pi_\theta(s,a))(r + \gamma V_v(s^\prime)-V_v(s))]$

目前，讲解的全是TD(0)，后面可以扩展为 $TD(\lambda)$ ，这里就不一一展开，详情可以参考教材，最后给出本将总结，

实验

小车爬坡（连续版本）中的数据显示，如果不用RBF作特征，收敛会比较慢，并且最优解也比较差。RBF虽然计算量大，但是在维度较少清苦下，对收敛速率的影响还是非常明显。

参考资料

《强化学习》第七讲策略梯度