这一讲的David授课视频与Sutton教材有所不同，将教材的5,6,7三章的前面一部分合并为一讲，主要内容介绍无模型的策略评估。没有模型就需要在经验中学习，本讲介绍两大方法

  • Monte-Carlo Evaluation
  • Temporal-Difference Evaluation

它们都是基于样本数据评估状态函数，并且有很强的内在联系。

Monte-Carlo学习算法

主要特点

  • MC直接重阶段性经验中学习。数据必须为阶段（Episode）形式。
    • 每一段数据必须有结束。
  • MC无需知道转移矩阵和奖励向量。
  • MC不会用其他预估的值函数计算当前值函数
  • MC使用均值估计值函数。

核心概念

目标：在策略$\pi$下，从阶段性的经验中学习$v_{\pi}$,数据形式如下

\[S_1^{(1)},A_1^{(1)},R_1^{(1)},\cdots,S_{k_1}^{(1)} \sim \pi \\ \cdots \\ S_1^{(n)},A_1^{(n)},R_1^{(n)},\cdots,S_{k_n}^{(n)} \sim \pi \\\]

回报函数定义，$G_t = R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{t-1} R_T$，$T$表示结束状态

值函数是回报函数的期望，$v(s)=E[G_t \vert S_t=s ]$

MC策略评估使用回报的经验均值作为值函数的无偏估计。评估策略有两个，

  • First-Visit
  • Every-Visit

下面以First-Visit为例，Every-Visit唯一的区别是在每个阶段内，状态s每次出均统计而不是只统计第一次，first-Visit的效率已经很低了，Every-Visit的效率更低。

  • 评估$v(s)$
  • 状态s第一次出现的t步
  • 状态s计数器$N(s) = N(s) + 1$
  • 状态s总回报$S(s) = S(s) + G_t$
  • 统计值$V(s)=S(s)/S(s)$
  • 根据大数定理，当$N(s) \rightarrow \infty$时， $V(s) \rightarrow v_{\pi}(s)$

均值增量式更新

\[\begin{align} u_k &= \frac{1}{k} \sum_{j=1}^k x_j \\ &= \frac{1}{k} \left(x_k + \sum_{j=1}^{k-1} x_j \right) \\ &= \frac{1}{k} \left(x_k + (k-1)u_{k-1} \right) \\ &= u_{k-1} + \frac{1}{k}(x_k - u_{k-1}) \\ \end{align}\]

将MC的计算，使用增量式更新表示，

\[\begin{align} & N(S_t) = N(S_t) + 1 \\ & V(S_t) = V(S_t) + \frac{1}{N(S_t)}(G_t - V(S_t)) \end{align}\]

在状态函数非固定(non-staionary)的场景，通常将系数$\frac{1}{N(S_t)}$用常量$\alpha$代替，

\[V(S_t) = V(S_t) + \alpha(G_t - V(S_t))\]

以上这种形式，可以非常方便的与TD算法比较。具体实现代码和实验效果参考这里。

Temporal-Difference学习方法

核心思想

  • TD无需知道转换矩阵和奖励向量
  • TD可以从不完全的阶段数据学习，而不像MC那样必须等待每个阶段结束在学习
  • TD通过其他的状态函数估计，更新当前的状态函数

最简单的TD算法记作$TD(0)$，更通用的写法为$TD(\lambda), \lambda \in [0,1]$，后面再展开，现在先关注$TD(0)$。更新算法为

\[V(S_t) = V(S_t) + \alpha(R_{t+1} + \gamma V(S_{t+1}) - V(S_t))\]

其中，$R_{t+1} + \gamma V(S_{t+1})$是TD目标，该值区别于非固定MC更新算法的$G_t$，它不需要等待阶段结束，直接通过下一个状态更新即可，所以非常方便。$\delta_t = R_{t+1} + \gamma V(S_{t+1}) - V(S_t)$称为TD error。具体实现代码和实验数据参考这里。

TD与MC的比较

  • 数据区别：TD无需等待阶段数据完成，既可学习；MC必须等待阶段数据完成；
  • 计算效率：TD实时性好于MC，TD收敛更快；
  • 模型效果：MC无偏估计，方差大；TD有偏估计，但是方差小，可以参考10000组21点实验对比。

Monte-Carlo，Temporal-Difference和Dynamic Programming更新比较

MC更新方式：需要阶段结束，$G_t$统计到结束为止， \(V(s_t) = V(s_t) + \alpha(G_t-V(S_t))\)

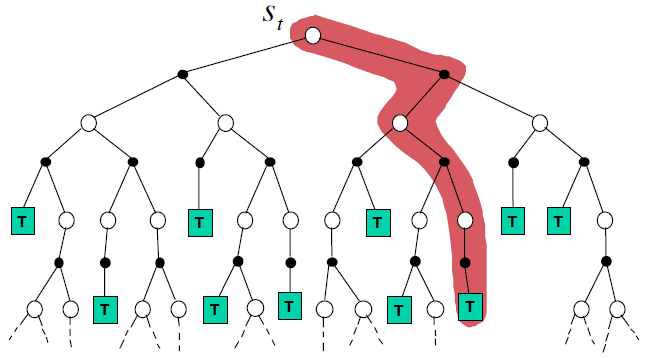
TD更新方式：只需要后面一个状态的信息即可，无需采样到底 ，

\[V(s_t) = V(s_t) + \alpha(R_{t+1} + \gamma V(s_{t+1}) - V(s_t))\]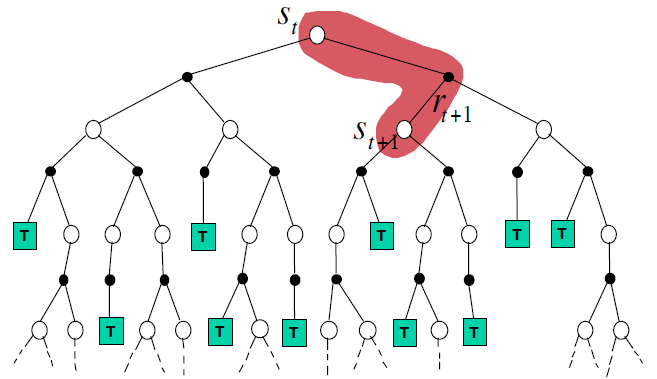

DP更新方式：需要全量信息，即转换矩阵和转换奖励，

\[V(s_t) = E_{\pi}[R_t + \gamma V(s_{t+1})]\]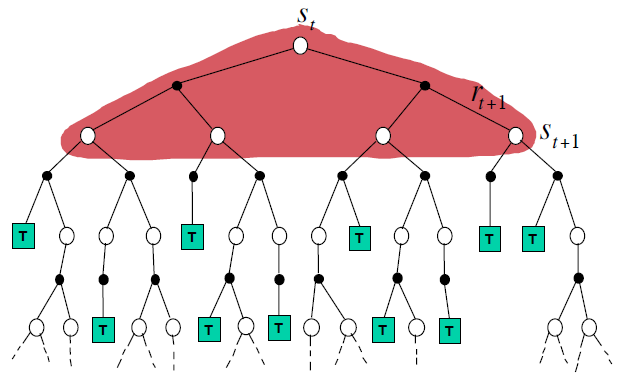

Bootstrapping和Sampling两个核心动作，DP，MC与TD的区别

  • Bootstrapping：使用其他预估更新当前状态函数
    • DP: YES
    • MC: NO
    • TD: YES
  • Sampling：使用随机样本更新当前状态函数
    • DP: No
    • MC: Yes
    • TD: Yes

其实，TD，MC与DP可以用下面这幅图表示，他们三个分别在三个角落，右上角是理想状态。

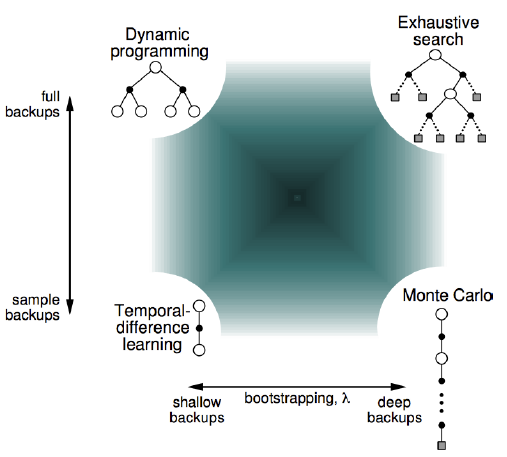
可以看到，TD与MC是有联系，左下角是$TD(\lambda)$，随着$\lambda$变大，可以逐渐变为MC。

n步回报 n-Step Return

定义如下

\[G_t^{(n)} = R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{n-1}R_{t+n} + \gamma^nV(S_{t+n})=\left(\sum_{k=1}^{n-1} \gamma^{k-1}R_{t+k}\right) + \gamma^nV(S_{t+n})\]
  • 当$n=1$时,$G_t^{(1)} = R_{t+1} + \gamma V(S_{t+1})$，之前提到的TD中对应的reward。
  • 当$n=\infty$时，$G_t^{(\infty)}=R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{T-1}R_T$，之前提到的MC中对应的reward

所以，从reward角度来看，TD与MC是两个极端。可以定义更为一般的学习算法：n-step TD

\[V(S_t) \leftarrow V(S_t) + \alpha(G_t^{(n)} - V(S_t))\]

$\lambda$回报

n-step TD中，什么n最好呢？一种中庸的办法是将所有n都试一遍，然后计算平均值。另一种方法是计算加权平均值，权重定义定义如下

\[G_t^{\lambda} = (1-\lambda)\sum_{n=1}^{T-t-1} \lambda^{n-1} G_t^{(n)} + \lambda^{T-t-1} G_t , \lambda \in [0,1]\]

系数之和为1，越近，权重越高,即$\lim_{n \rightarrow\infty}(1-\lambda)\sum_{n=1}^\infty \lambda^{n-1} = 1$。将该定义推广到TD，可表示为$TD(\lambda)$，更新方法为

\[V(S_t) \leftarrow V(S_t) + \alpha (G_t^{\lambda} - V(S_t))\]

TD(0)就是之前提到的TD，TD(1)就是MC。这种方法也称之为前向视图，教材中还讨论到后向视图，该视图主要是用于高效算法，无需等待结束，每一次交互，均可以计算出现有阶段z之前的的所有（或部分）$G_t^\lambda$。