本文主要介绍LSH的整个工作原理，并结合欧式距离给出实例。

$(r_1,r_2,p_1,p_2)-sensitive$

LSH的核心工作原理就是找到一组hash函数，它们必须符合$(r_1,r_2,p_1,p_2)-sensitive$条件。这类函数定义：$H=\lbrace h: S \rightarrow U \rbrace$，对于任意一种距离度量方法D，任意向量$q,v \in S$

\[如果 v \in B(q, r1), P(h(v)=h(q)) \ge p1 \\ 如果 v \notin B(q, r2), P(h(v)=h(q)) \le p2\]

其中$B(v,r) = \lbrace q \in X | d(v,q) \le r \rbrace$，表示以点$v$为中心，距离为r范围内的所有点的集合。

上面定义的直观解释就是Locality Sensitive Hashing。 即将相距较近($r_1$以内)的向量hashing到一起的概率要大($p_1$较接近1)；距离较远($r_2$以外，且$r_2 > r_1$)的对象hashing到一起的概率小($p_2​$较接近0)。

欧式空间中的$(r_1,r_2,p_1,p_2)-sensitive$应用

在上一篇文章LSH在欧式空间的应用(1)–碰撞概率分析中讨论的投射方法和碰撞概率函数，就是分别对应上面定义的$h$和$P$。尤其是碰撞函数，可以根据给出的$r_1$和$r_2$情况估算$p_1$和$p_2$，并且计算最优的$w$的范围。首先，回顾一下碰撞函数，

\[P(h(v)=h(q)) = g(c) = 1 - 2F(-\frac{1}{c}) + \sqrt{\frac{2}{\pi}}c(e^{-\frac{1}{2c^2}}-1)\]

其中$c=\frac{u}{w}$,假设$r_1=5,r_2=50,p_1 = 0.95, p_2 = 0.1$。根据碰撞概率的解析公式，可以得到$p_1,p_2$对应的数值解。即$c_1 = g^{-1}(p_1),c_2=g^{-1}(p_2)$。由于概率公式是减函数，所以

\[\begin{align} g(c_1) \ge p_1 且 g(c_2) \le p_2 &\Rightarrow c_1 \le g^{-1}(p_1) 且 c_2 \ge g^{-1}(p_2) \\ &\Rightarrow \frac{r_1}{w} \le g^{-1}(p_1) 且 \frac{r_2}{w} \ge g^{-1}(p_2) \\ &\Rightarrow \frac{r_1}{g^{-1}(p_1)} \le w \le \frac{r_2}{g^{-1}(p_2)} \\ &\Rightarrow \frac{5}{g^{-1}(0.95)} \le w \le \frac{50}{g^{-1}(0.1)} \\ \end{align}\]

$p_1,p_2与r_1,r_2$可以根据应用精度和数据范围，人工估算。通过碰撞公式，完美的解决了$w$的取值问题，非常具有指导意义。但是，上述不等式不是永远成立的，部分$p_1,p_2与r_1,r_2$的组合可能导致不等式下界大于上界。

强化LSH函数

强化LSH函数，可以不改变LSH算法的情况下，通过增加运算量，提高精度。假设有一个$(r_1,r_2,p_1,p_2)-sensitive$函数族$F$，可以通过逻辑与的方法构造一个新的函数族$F’$。

假设$f \in F’$并且$f_i \in F, i = 1,2,\cdots r$。令$f(x)=f(y)$为$f_i(x)=f_i(y),i = 1,2,\cdots,r$，此时$F’$是$(r_1, r_2, p_1^r, p_2^r) - sensitive$。如果$p_2$较小,$p_1$较大，可以通过此操作将其进一步的缩小，同时有不会将$p_1$变得太小。

同理，可以使用逻辑或的方法，将其变成一个$(r_1, r_2, 1-(1-p_1)^r, 1-(1-p_2)^r) - sensitive$。其效果与逻辑和相反，它将概率均变大。

常用的方法是将逻辑与嵌套到逻辑或中使用，得到$(r_1, r_2, 1-(1-p_1^k)^L, 1-(1-p_2^k)^L) - sensitive$函数族（先使用逻辑与，再使用逻辑和也可）。这种组合的意义是去掉那些碰巧hash到一起的情况，如果真的很近，在L组计算中，总有一组k个hash均相等。k和L需要设置合理，L如果设置太大，计算开销会增加。给定k，增强的概率比原来要好，即$\rho_1 \le 1-(1-p_1^k)^L, \rho_2 \ge 1-(1-p_2^k)^L$，可以得到L的范围:

\[\frac{\ln{(1-\rho_1)}}{\ln{(1-p_1^k)}} \le L \le \frac{\ln{(1-\rho_2)}}{\ln{(1-p_2^k)}}\]

L取范围内最小的整数，节省空间。桶里，上面不等式不保证永远成立，条件太苛刻时需要调整。

LSH的工作流程

前面理论讲了很多，现在介绍LSH的工作流程。大体步骤分为两步：1）创建hash表；2）对象聚集。

创建hash表

如果不使用增强hash函数，理论上只需要一个hash表即可。但是从实际应用来看，一个hash表要不够精确。最佳实践是创建$k \times L$个hash表，每一个表的hash函数均是使用标准正太分布随机生成投影向量和均匀分布生成随机偏移量。每k个hash表为一组，称为一个“桶”，共L个桶。生成过程如下：

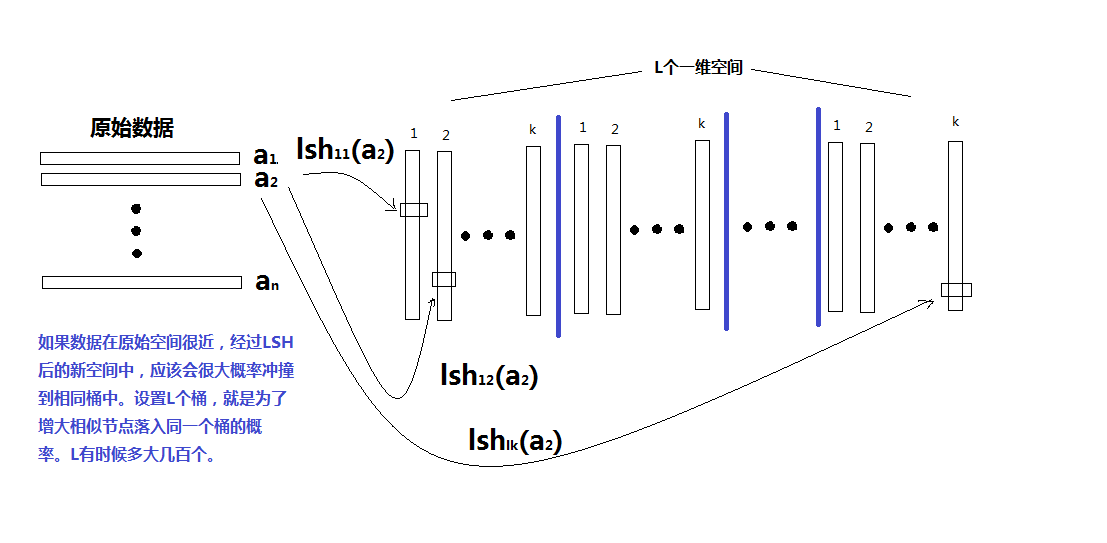
由于随机的原因，可能有些比较近的对象在一个桶内会hash到不同的位置，但是我们给了L个桶，即L此碰撞机会。如果他们真的相似，总有可能在其他桶里面hash到同一个位置（该桶内所有k个hash值均相等）。

对象聚集

hash表创建完毕后，只是给每个对象一堆($k \times l$)标记，实际上相似的对象并没有在一起。需要将这些标记，每k个合并为一个id，然后按照id聚合。生成id使用两段hash函数$h_1$和$h_2$,计算方法如下

\[h_1 = a \bullet v \bmod p \bmod n \\ h_2 = b \bullet v \bmod p\]

其中$a,b \in R^k$,且$a_i,b_i是随机整数$。$p$是一个很大的质素，通常$p=2^{32}-5$；n是源数据条数。如果只使用1个hash函数，n较大时，冲撞的概率不可以忽略；但是如果使用两个hash函数，冲撞的概率基本可以忽略不计。整个过程示意图如下：

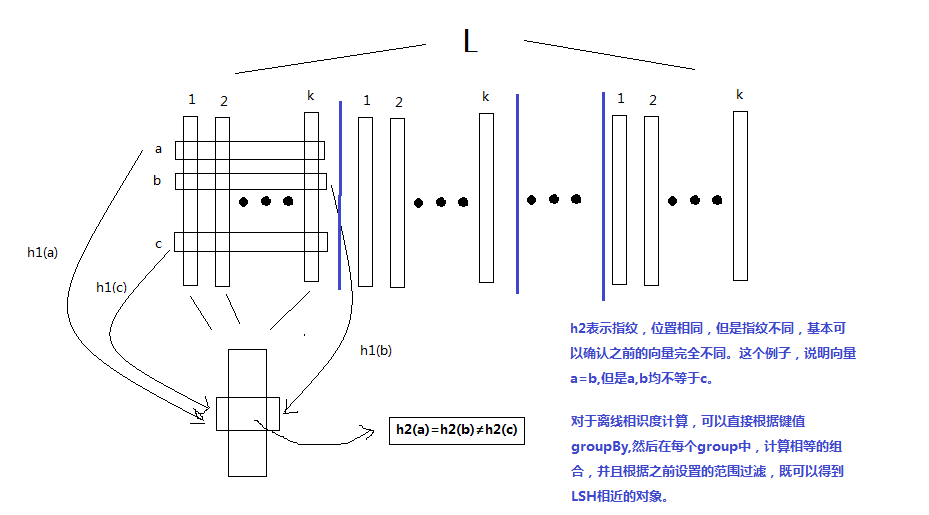
合并后，同一个key下的所有对象就是比较近的对下。然后根据事先设定的相似度阀值，得到阀值以内的相似对象。

参考文献