矩阵的四个线性子空间是线性代数的理论基石，包含了线性子空间，矩阵的秩，维度，基，零空间，逆等。下面的内容总结相关内容，作为备忘，方便后续快速回顾。

四个子空间及性质

设$r = rank(A)$,矩阵A的维度为$m \times n$, dim为计算空间的维度

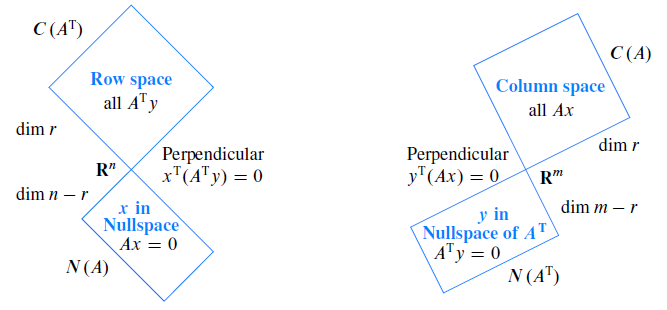
  • $列空间=C(A), dim(C(A))=r$
  • $行空间=C(A^T), dim(C(A^T))=r$
  • $零空间=N(A), dim(N(A)) = n-r$
  • $左零空间=N(A^T), dim(N(A^T))=m-r$

根据零空间定义，上面四个空间，两个互为垂直（即一个空间中的任意向量与另一个空间任意向量点积为0）：$C(A) \perp N(A^T), C(A^T) \perp N(A)$

为什么$r=dim(C(A))=dim(C(A^T))$

行空间维度 矩阵秩r为轴列(pivot coloumn)的个数，而当A通过消元转成R时($EA = R$)，轴的个数可以通过非0行的数量得到，也就是前r行。而前r行中，轴列组成了单位矩阵$I_{r \times r}$，所以$C(A^T)$的基是前R行，其维度为r。

列空间维度 在计算零空间时，通过消元，可以得到$A\vec{x}=0 \Leftrightarrow R\vec{x}=0$。对于最简行矩阵R，其列空间是轴列，由于消元过程不改变列的位置，所以A的轴列与R一致。根据R的结构，发现R的轴列可以线性的表示R的其他自由列，所以R的轴列支撑$C(R)$，且维度为r。由于使用相同的系数$\vec{x}$，A的轴列同样可以表示$A$的其他列，所以$A$的轴列支撑$C(A)$，维度为r。

例子：计算矩阵的四个线性子空间

设矩阵A如下

\[A = \begin{bmatrix} 1&3&0&5 \\ 2&6&1&16 \\ 5&15&0&25 \end{bmatrix} = \begin{bmatrix}1&0&0 \\ 2&1&0 \\ 5&0&1 \end{bmatrix} \begin{bmatrix} 1&3&0&5 \\ 0&0&1&6 \\ 0&0&0&0 \end{bmatrix} = LU = E^{-1}R\]

四个线性子空间基为

  • 列空间

\(s_1=E^{-1}R[,1] =\begin{bmatrix}1&0&0 \\ 2&1&0 \\ 5&0&1 \end{bmatrix} \begin{bmatrix} 1 \\ 0 \\ 0 \end{bmatrix} =\begin{bmatrix} 1 \\ 2 \\ 5 \end{bmatrix}\), \(s_2=E^{-1}R[,3] =\begin{bmatrix}1&0&0 \\ 2&1&0 \\ 5&0&1 \end{bmatrix} \begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix} =\begin{bmatrix} 0 \\ 1 \\ 0 \end{bmatrix}\)

  • 行空间

$s_1=R[1,]=\begin{bmatrix} 1&3&0&5 \end{bmatrix}^T,s_2=R[2,]=\begin{bmatrix} 0&0&1&6 \end{bmatrix}^T$

  • 零空间

先交换R的2,3列，得到形式\(\begin{bmatrix}I&F \\ 0&0 \end{bmatrix}\)，然后根据块公式得到零空间矩阵\(\begin{bmatrix}-F \\ I\end{bmatrix}\)，最后交行2,3行，得到最终结果。$s_1=\begin{bmatrix}-3&1&0&0\end{bmatrix}^T,s_2=\begin{bmatrix}-5&0&-6&1\end{bmatrix}^T$

  • 左零空间

根据左零空间的定义，即是$A^T\vec{y}=\vec{0} \Leftrightarrow \vec{y}^TA=\vec{0}^T$，也就是消元$EA$过程中得到R零行对应的E的行，即$s_1=E[3,]=\begin{bmatrix}-5&0&1\end{bmatrix}^T$

通过上面的过程，可以发现只需要通过消元，就可以得到四个线性子空间的重要信息，基与维度。消元的原理虽然简单，但是其意义不简单，它好比剥洋葱，将皮一层层去掉，得到最后不变的内核。