背景

在网络理论的研究中，复杂网络是由数量巨大的节点和节点之间错综复杂的关系共同构成的网络结构。用数学的语言来说，就是一个有着足够复杂的拓扑结构特征的图。复杂网络的研究是现今科学研究中的一个热点，与现实中各类高复杂性系统，如的互联网、神经网络和社会网络的研究有密切关系。

复杂网络通常是有数以亿记的边与节点组成，导致需要处理的数据量非常庞大，即使是计算简单的网络属性都需要耗费很高的计算资源和存储空间。本文介绍复杂网络介数和直径的方法：介数使用估算方法，可以将误差控制在可接受范围；后者使用启发式方法，精准计算直径，在小世界网络上有不错的效果。

介数

指标定义

介数（betweenness）可分为点介数和边介数，

  • 节点介数定义为网络中所有最短路径中经过该节点的路径的数目占最短路径总数的比例，
  • 边介数定义为网络中所有最短路径中经过该边的路径的数目占最短路径总数的比例。

介数用于衡量一个点或边的重要程度，值越高，该点或边越重要（后面的讨论均是针对点介数，边介数实现方式类似）。该指标虽然好，但是计算开销非常之大，如果没有优化，纯粹按照定义计算，复杂度为$O(n^3)$(n是节点数)，定义如下:

\[Bet(v) = \sum_{s \ne t \ne v \in V}\frac{\sigma_{st}(v)}{\sigma_{st}}\]

其中 $\sigma_{st}$ 是s，t之间最短路径的数量，$\sigma_{st}(v)$ 是s，t最短路径中包含节点v的数量。

根据Brandes的快速介数计算，可以将复杂度降到$O((m+n)n)$(m，n分别是边数和节点数)。但是，即使是spark，面对此计算量计算上百万节点的图仍然不太现实。所以，只能估算每个点的介数。最后，采用Brandes的介数估算算法，使复杂度降到可接受的$O(m+n)$。虽然牺牲了部分精度，但是在样本达到一定数据量时，误差可以降到可接受的范围。

估算方法

首先需要从精确计算介数谈起，首先定义一个变量，称之为dependency，简单来讲，在原始定义中，将源点s固定，v和t变化，形式的定义如下：

\[\delta_{s\bullet}(v) = \sum_{t \ne v \in V} \frac{\sigma_{st}(v)}{\sigma_{st}}\]

Brandes的快速介数计算算法中，每计算一轮会将所有v针对固定源点s的dependency计算出来，计算n轮，然后针对每个v，合并所有dependency，就可以计算每个点介数值。介数估算的方法是随机抽取k节点，计算对应的dependency，然后计算每个v的平均dependency并乘以n，得到最终估算结果。

理论依据是霍夫丁不等式，相同分布的独立随机变量$X$有界 ${0 \le X \le M}$，样本均值与期望的关系，如下：

\[P(| \overline{X} - E(X)| \ge \xi)\le e^{-2k(\frac{\xi}{M})^2}\]

介数近似计算中，$X=Dependency$，$M=n-1$。由于$k\ll m$，所以最终复杂度不变。以上就是计算介数估算的大体框架，具体细节请参考Brades介数估算论文，里面有估算的误差估计证明以及实验效果。

实现

使用spark的pregel实现了整个逻辑。需要计算k轮，每一轮的计算量包括

  • 一个单源最短路径，
  • 一个前置节点搜集，
  • 一个依赖合并过程

总共需要三个pregel过程和一个vertexLeftJoin过程，每一轮的复杂度为$O(m+n)$。k可以认为是常数，所以整体复杂度为线性。 经过几轮优化，计算效果有了大幅度提升。使用100个executor，2核，每个executor 14G内存，对450,000,000点，1,253,792,736 边的图，随机迭代5轮，需要一千多分钟，每轮平均200分钟。

直径

图论中，图的直径是指任意两个顶点间距离的最大值。距离是两个点之间的所有路的长度的最小值。所以，按照定义计算直径，复杂度为$O(n^3)$。大型网络上，此指标基本无法计算。这次介绍一种启发式直径计算方法，实验证明该方法在小世界网络上收敛非常快。

算法思路

根据当前点的离心率，推断所有其他点的离心率。由于直径等于最大离心率，根据启发式规则(启发式规则有很多，具体可以参考原始论文)搜索其他节点的上下界，可以不断缩小直径的上界和下界，同时排除掉那些对上界和下界没有贡献的点。最终得到精确的直径，相关理论推导，可以参考图直径与离心率(eccentricity)相关推论。

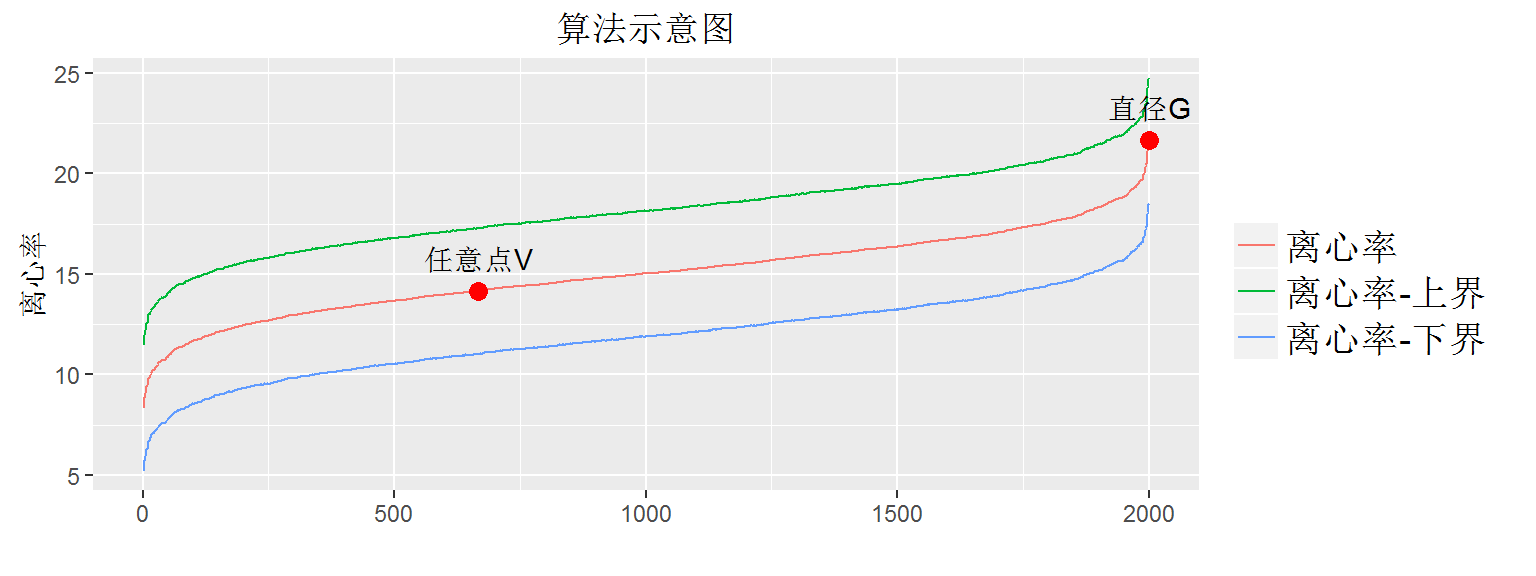
实验效果

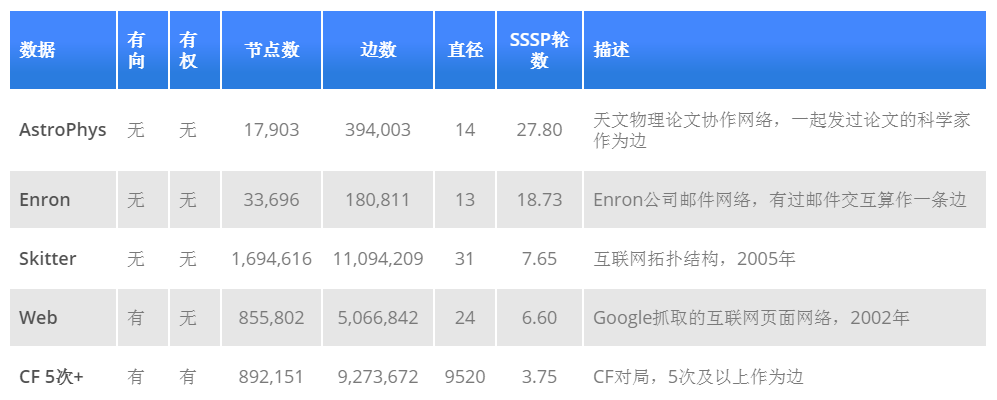
以上试验使用R单机实现，每一组数据均试验20轮，取平均需要的SSSP轮数。SSSP轮数相比于节点数，基本上可以忽略不计。选取天体物理论文网络，直径上下界收敛非常快，观察如下

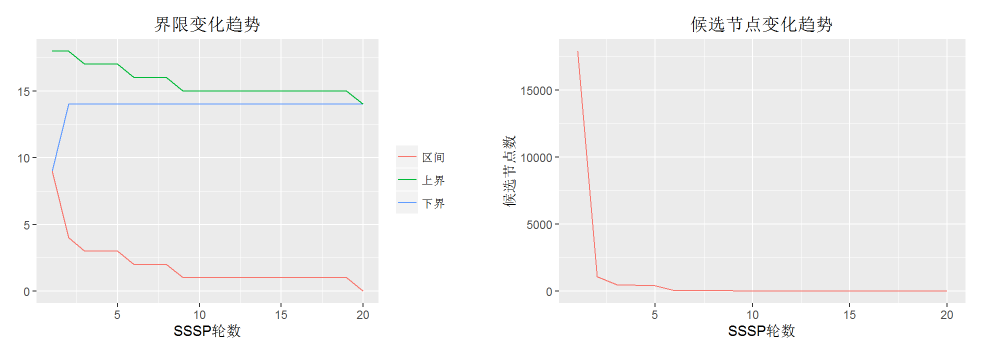
可以发现，只用了不到5轮，候选节点急剧减少，上下界区间也非常接近于0。

我们使用spark实现了一个版本，发现在部分图上，数据收敛并没有实验中那么快，可能是这些图不具备小世界图的一些属性。但是上下界却收敛得非常接近，所以即使无法精确计算直径，也可以在有限的迭代次数中得到直径的近似估计。

总结

复杂网络的计算，原始复杂度一般都非常高，在上亿节点的图中基本无法计算，所以常用的方法是估算。本文分别介绍了复杂网络介数和直径的估算方法。使用spark实现，并验在真实数据证了这些理论。

参考资料